Teorema di Cholesky

Requisiti

Matrice simmetrica definita positiva. La fattorizzazione è quindi semplificata perché non serve pivoting (vedi Stabilità) e si può lavorare solo sul triangolo inferiore.

Il metodo di Cholesky è una variante del Metodo di Gauss, caso particolare di $A=LU$, variante della fattorizzazione $A=LD{L}^T$, o Fattorizzazione matrici simmetriche.

Stabilità

Metodo efficiente e stabile numericamente e quando applicato a matrici simmetriche positive.

Una matrice simmetrica $A\in {\mathbb{R}}^{n\times n}$ è definita positiva se e solo se esiste una matrice triangolare inferiore $\mathcal{L}$ con elementi diagonali positivi tale che $A={\mathcal{LL}}^T$.

Dopo opportuni calcoli, si può ottenere la tesi ponendo $\mathcal{L}=L\Delta$, con $\Delta$ matrice diagonale con elementi $\sqrt{d_{ii}}$.

Algoritmo di fattorizzazione

$$A=LD{L}^T={\mathcal{LL}}^T$$

Si indicano con ${\ell }_{jk}$ gli elementi di $\mathcal{L}$. Dal momento che $\mathcal{L}=L\Delta$, si ha:

• ${\ell }_{jj}=\sqrt{d_{jj}}$
• ${\ell }_{jk}=l_{jk}\sqrt{d_{kk}},\forall k=1,...,j-1$

Seguendo le regole di pavimentazione della Fattorizzazione matrici simmetriche $LD{L}^T$, si ottiene l’algoritmo di Cholesky sostituendo le relazioni precedenti con

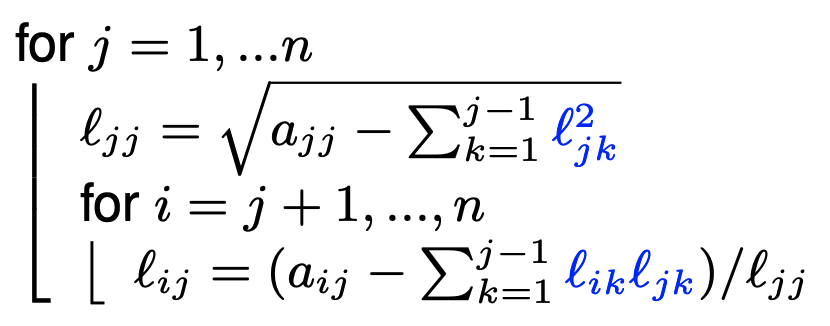
Stabilità

Si può dimostrare che se A è definita positiva, allora i pivot soddisfano automaticamente la condizione di pivoting parziale.

La stabilità, rispetto al Metodo di Gauss, è più forte, perché gli elementi vengono maggiorati da costanti che non dipendono dalla dimensione della matrice.

Algoritmo di default in Matlab utilizzando l’operatore "" per le matrici simmetriche.