Pattern matching

Alfabeto: insieme finito di caratteri $\sum =\{c_1,c_2,...,c_m\}$ Stringa su alfabeto: sequenza lineare di elementi di $\sum$, $\alpha =s_0,s_1...s_n:\forall i=0,...,n\text{mbox}{s}_i\in \sum$ Insieme di stringhe definite su $\sum$: $\sum \ast$ insieme di tutte le stringhe di lunghezza finita sull’alfabeto $\sum$.

title: Esempio
- $\sum = \{0, 1\}$, con stringa $\alpha = 0100011101010$ numero binario. $\sum \ast$ è l'insieme di numeri binari di qualunque lunghezza
- $\sum=\{a, c, g, t\}$ con stringa $\alpha=acctgtca$ porzione di DNA

La stringa vuota è definita con $ϵ$. $\beta$ è una sottostringa di $\alpha$ se esistono due stringhe $\gamma ,\delta$ eventualmente vuote tale che $\alpha =\gamma \beta \delta$. $\alpha =\gamma \beta$, $\gamma$ è prefisso di $\alpha$ $\alpha =\beta \delta$, $\delta$ è suffisso di $\alpha$

Concatenazione

Date due stringhe $\alpha$ e $\beta$ sullo stesso alfabeto $\sum$, la concatenazione è $\gamma =\alpha \beta$ data dalla giustapposizione di $\alpha$ e $\beta (|\gamma |=|\alpha |+|\beta |)$ $\alpha =\text{mbox}IPPO,\beta =\text{mbox}POTAMO$ $\gamma =\text{mbox}IPPOPOTAMO$

Potenza

Data una stringa $\alpha$ su un alfabeto $\sum$, la potenza k-esima è la concatenazione di $\alpha$ con se stessa k volte $\alpha =\text{mbox}PIPPO$ ${\alpha }^3=\text{mbox}PIPPOPIPPOPIPPO$

Occorrenza

Se $\beta$ è una sottostringa di $\alpha$, allora $\alpha$ contiene almeno un’occorrenza di $\alpha =\text{mbox}ALGORITMI,\beta =\text{mbox}ORI\to \gamma =\text{mbox}ALG,\delta =\text{mbox}TMI$

Se $\alpha =\gamma \beta \delta$ e $|\gamma |=k$, $\beta$ occorre alla posizione k di $\alpha$ $\alpha =\text{mbox}ALGORITMI,\beta =\text{mbox}ORI\to \gamma =\text{mbox}ALG\text{mbox}e\delta =\text{mbox}TMI$, e $\beta$ occorre alla posizione 3 in $\alpha$.

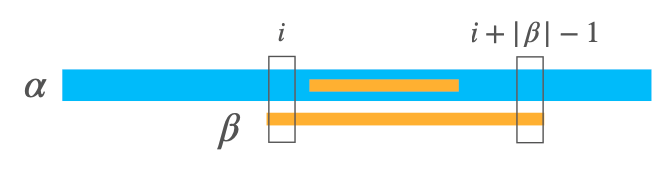
Allineamento

L’allineamento di una stringa $\beta$ alla posizione i della stringa $\alpha$ è la sovrapposizione ideale di $\beta$ con la sottostringa $\alpha [i..i+|\beta |-1]$.

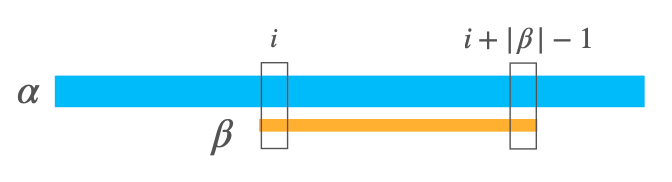
Allineamento con successo

Esiste un’occorrenza della stringa $\beta$ alla posizione i della stringa $\alpha$

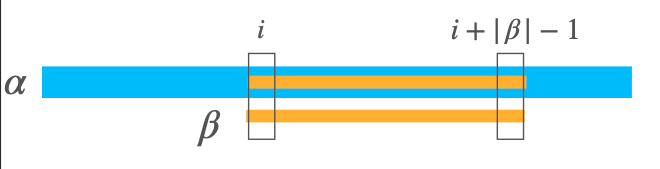
Allineamento fallito

Non esiste un’occorrenza della stringa $\beta$ alla posizione i della stringa $\alpha$

asd_43