Componenti connesse

Componente connessa $G^{\prime }$ è un sottografo connesso ed è massimale, ovvero non esiste un sottografo connesso di $G^{\prime \prime }$ di $G$ che includa tale che $G^{\prime }\subseteq G^{\prime \prime }\subseteq G$

Componente fortemente connessa $G^{\prime }$ è un sottografo fortemente connesso ed è massimale, ovvero non esiste un sottografo connesso di $G^{\prime \prime }$ di $G$ che includa tale che $G^{\prime }\subseteq G^{\prime \prime }\subseteq G$

Valutazione

Un grafo G è (fortemente) connesso?

Valutare, dato in input un grafo G (in)diretto, se G è (fortemente) connesso. 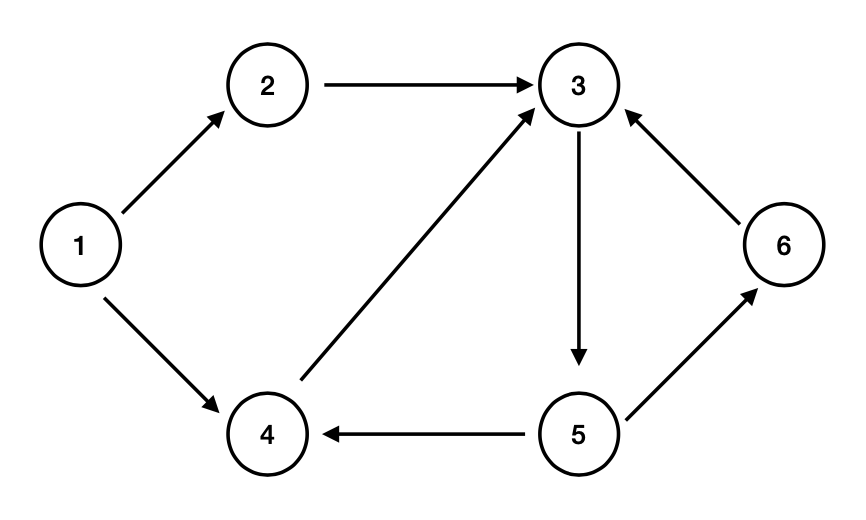Non è fortemente connesso perché non c’è un cammino diretto tra 6 e 1.

Quali sono le componenti fortemente connesse di un grafo G?

1. Eseguire una Visita in profondità, che ci restituisce un array di post.
2. Invertire tutti gli archi nel grafo ($G^T$)
3. Determinare la foresta di copertura su $G^T$ con una DFS considerando i nodi in ordine decrescente di post
4. Determinare le componenti fortemente connesse dalla foresta di copertura (albero === componente)
5. Restituire le componenti

Il costo di questo algoritmo è $O(|V|+|E|)+O(\text{mbox}calcolotrasposto)$

Spiegazione: Per ogni componente si crea un nodo. I nodi sono connessi se esisteva un arco nel grafo originale tra un nodo di una componente e un nodo dell’altra. Questo grafo che si è andato a creare è un DAG, perché non può avere cicli. Se avesse cicli, i nodi che fano parte del ciclo sarebbero un’unica componente.

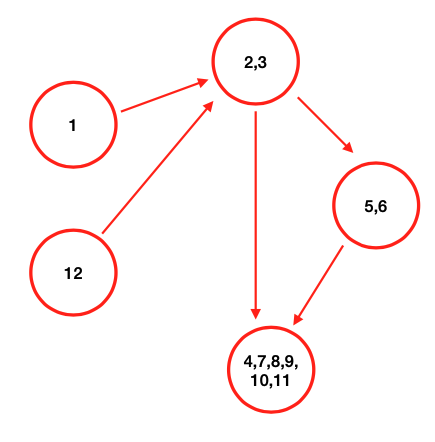
Dal momento che è un DAG, si può linearizzare.

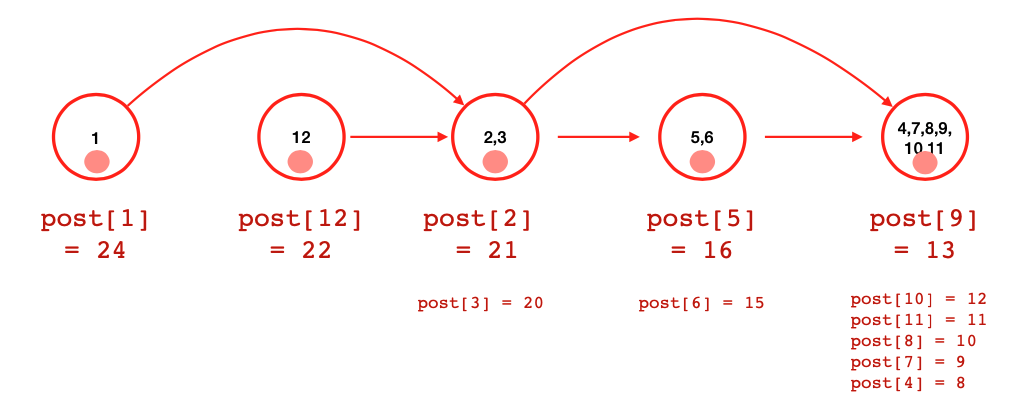
Proposizione Una componente fortemente connessa in G è una componente fortemente connessa in $G^T$.

Se esiste una componente fortemente connessa in $G^T$ non esistente in $G$, deve esistere anche in $G$.

asd_29