Minimum spanning tree

Albero di copertura completo senza cicli.

Input: Grafo $G=(V,E)$ indiretto connesso funzione di peso sugli archi di G $c:E\to \mathbb{R}$ Output: albero di copertura di peso minimo

L’albero di copertura è T per $G=(V,E)$: $T=(V,E^{\prime })$, tale che $E^{\prime }\subseteq E$, è un albero, quindi $|E^{\prime }|=|V|-1$.

Il peso dell’albero di copertura $T=(V,E^{\prime })$ per $G=(V,E)$ è dato da: ${\sum }_{e\in E}c(e)$

La soluzione ottima è la soluzione che ha il minimo peso possibile. Può non essere l’unica.

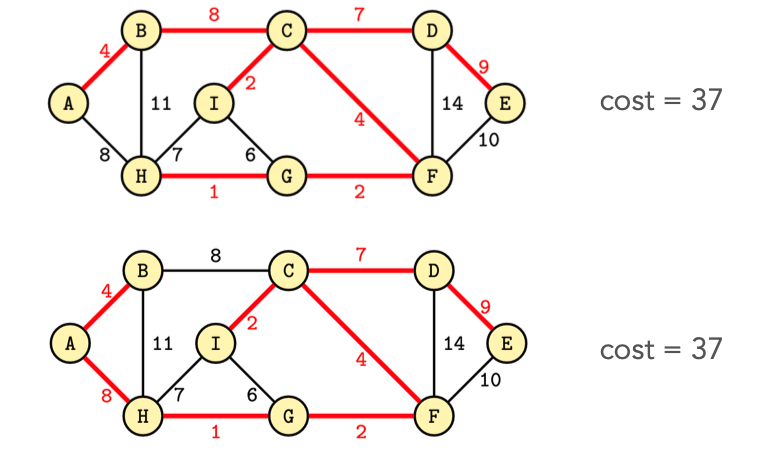
Il minimum spanning tree e l'albero dei cammini minimi non sono la stessa cosa. In entrambi i casi si hanno cammini di copertura, ma l'albero dei cammini minimi rappresenta il minimo di ogni cammino che sull'albero connette la sorgente ai nodi, mentre per il minimum spanning tree anche se è sempre un albero, cambia il costo e cambia anche il problema, perché mi basta la somma del costo degli archi.

Il minimum spanning tree ha una sottostruttura ottima. Togliendo un elemento dall’albero, sono sicuro che l’albero/i due alberi che rimangono sono a loro volta minimum spanning tree.

Entrambi gli algoritmi seguenti ritornano un albero di copertura.

title: Teorema
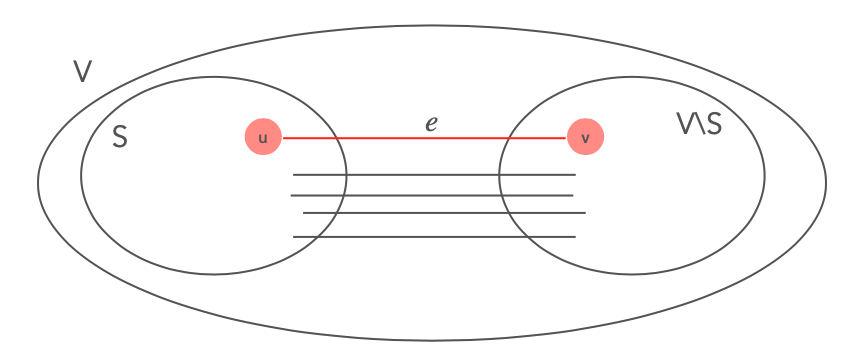
Dati un grafo $G=(V, E)$ e una funzione di costo $c: E \to R$ sugli archi, sia $S \subset V$ un sottoinsieme proprio e non vuoto di V ($0 \lt |S| \lt |V|$) e sia $e = (u, v) \in E$ un arco di costo minimo tale che $u \in S \mbox{ e } v\in V \setminus S$, allora l'arco $e$ appartiene a un MST per G.

La parte $(S,V\setminus S)$ è detta taglio del grafo G. L’arco $e$ è un arco di costo minimo che attraversa un taglio di G, ed è detto safe.

I seguenti algoritmi restituiscono anche un Minimum spanning tree, ovviamente, e ad ogni iterazione viene scelto un arco safe.

Algoritmo di Kruskal

$O(m\log n)$

1. ordina gli archi in ordine crescente di peso
2. sceglie gli archi del MST iterativamente. Ad ogni iterazione sceglie l’arco di peso minimo che non crea cicli
3. termina quando tutti i nodi sono connessi

Per capire se si sta formando un ciclo, su utilizza il disjoint set. Se due nodi sono già nello stesso sottoalbero, allora si andrà a formare un ciclo. Si termina quando si sono selezionati $n-1$ archi.

Kruscal(G, c):
	S := make_set(V) # disjoint set
	T := new_list()

	ordina gli archi in E in modo crescente in base a c
	count := 0
	while count < n-1 do
		prossimo arco (u, v) ∈ E
		if find-set(S, u) != find-set(S, v) then
			p := new_list_node()
			p.val := (u, v)
			insert-head(T, p)
			union(S, u, v)
			count := count + 1
	return T

Il costo totale è di $O(m\log n)$.

Algoritmo di Prim

$O(m\log n)$ L’idea è simile all’albero dei cammini minimi.

1. sceglie un nodo sorgente
2. costruisce un MST incrementalmente. Ad ogni iterazione sceglie l’arco di peso minimo che unisca un nodo non ancora nell’albero ad un nodo già nell’albero
3. termina quando tutti i nodi sono connessi

Si deve tenere traccia dei nodi nel MTS e del costo degli archi. Per scegliere il nodo in ogni iterazione si implementa una coda con priorità.

Prim(G, c):
	for all v ∈ V do
		cost[v] := +∞
		prev[v] := nil
		S[v] := 0 # sta o meno nell'albero
	nodo s in V
	cost[s] := 0
	S[s] := 1

	Q := make_priority_queue(V') # coppie di nodi di V e cost[]

	while not is_empty_queue(Q) do
		u := dequeue(Q)
		S[u] := 1

		for all (u, v) ∈ E do
			if S[v] = 0 and cost[v] > c(u, v) then
				cost[v] := c(u, v)
				prev[v] := u
				decrease_priority(Q, v, cost[v])
	return prev[]

Il costo totale dell’algoritmo di Prim è $O(m\log n)$

asd_36