Alberi binari

Un albero binario è un albero in cui ogni nodo ha zero, uno o due figli, i quali vengono identificati come figlio sinistro e figlio destro. I figli sono definiti dalla struttura dell’albero e non possono essere scambiati.

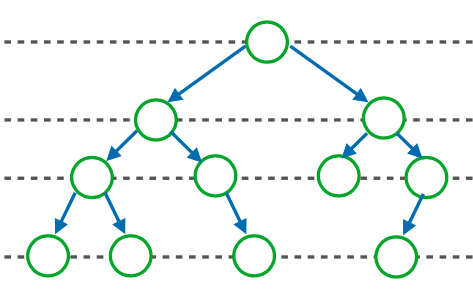
Albero completo Un albero binario è completo se ogni nodo ha zero o due figli, ovvero non esiste nessun nodo con un figlio.

Albero bilanciato Un albero binario è perfettamente bilanciato se le foglie sono tutte allo stesso livello.

title: Proposizione
Un albero binario completo e perfettamente bilanciato di altezza $h \ge 0$ ha esattamente $n=2^{h+1} - 1$ nodi di cui $2^h$ foglie.

La dimostrazione si fa per induzione. Caso base: un albero di altezza 0 ha $h=0$ e un solo nodo, quindi $2^{0+1}-1=1$, che è anche il numero di foglie. Ipotesi induttiva: Un albero di altezza $h-1\ge 1$ ha $2^{h-1}$ foglie. Passo induttivo: L’albero di altezza $h$ contiene un albero di altezza $h-1$, e quindi le sue foglie sono i nodi del penultimo livello dell’albero. Ogni nodo del penultimo livello ha esattamente due figli, che sono le foglie dell’albero. Il numero di figlie è quindi $2^{h-1}\cdot 2=2^h$.

Per ogni $i=0,...,h$, il numero di nodi al livello $i$ è uguale al numero di foglie di un albero binario completo perfettamente bilanciato di altezza $i$. Il numero totale di nodi è quindi ${\sum }_{i=0}^h{2}^i=2^{h+1}-1$

title: Corollario
Un albero binario completo e perfettamente bilanciato di $n$ nodi ha altezza $h=\log(n+1) - 1 \in \Theta(\log n)$.

Il nodo dell’albero binario è composto da un valore, il puntatore al figlio di sinistra e il puntatore al figlio di destra.

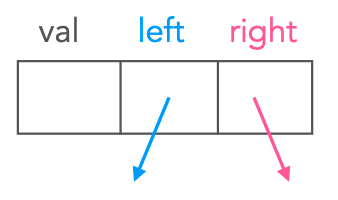
Esiste anche una variante con l’aggiunta di un puntatore al nodo padre.

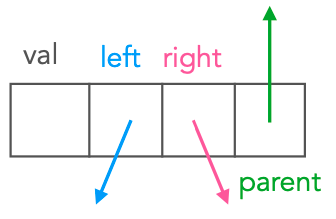
Visita alberi

Esistono due tipi di visita di un albero binario:

• Visita in profondità (DFS, Depth First Search)
• Visita in ampiezza (BFS, Breadth First Search)

Il costo computazionale delle visite è $\in O(n\cdot f(n))$, dove $O(f(n))$ è il costo della visita del nodo.

Visita in profondità - DFS

Si visitano ricorsivamente i sottoalberi, ed esistono tre varianti:

1. pre-order: il nodo viene visitato prima di visitare i sottoalberi dei figli
2. in-order: il nodo viene visitato dopo aver visitato il sottoalbero del figlio di sinistra ma prima di visitare il sottoalbero del figlio di destra
3. post-order: il nodo viene visitato dopo aver visitato i sottoalberi dei figli

Per questo algoritmo si utilizza la ricorsione, quindi implicitamente uno stack come struttura dati.

DFS_pre_order(L):
	if L != nil then
		print(L.val)
		DFS_pre_order(L.left)
		DFS_pre_order(L.right)

DFS_in_order(L):
	if L != nil then
		DFS_pre_order(L.left)
		print(L.val)
		DFS_pre_order(L.right)

DFS_in_order(L):
	if L != nil then
		DFS_pre_order(L.left)
		DFS_pre_order(L.right)
		print(L.val)

Visita in ampiezza - BFS

Si visita un livello dopo l’altro, partendo dalla radice. In questo caso si utilizza una coda esplicitamente.

BFS(L):
	if L != nil then
		q := new_queue()
		enqueue(q, L)
		while !is_empty_queue(q) do
			n := dequeue(q)
			print(n.val)
			if n.left != nil then
				enqueue(q, n.left)

			if n.right != nil then
				enqueue(q, n.right)

asd_19asd_20