Heap binario

Min heap binario

Dato un insieme di chiavi totalmente ordinabile, un heap binario è un albero binario che memorizza chiavi dell’insieme:

• ogni nodo contiene una chiave
• l’albero è binario completo quasi perfettamente bilanciato a sinistra. È completo fino al penultimo livello, mentre all’ultimo livello le foglie sono ammassate a sinistra
• per ogni nodo v la chiave memorizzata è $\le$ delle chiavi memorizzate nel sottoalbero radicato in v

Max heap binario

È uguale al min heap binario, solo che per ogni nodo v la chiave memorizzata è $\ge$ delle chiavi memorizzate nel sottoalbero radicato in v.

Proprietà

Un heap con $n$ nodi ha altezza $h=\lfloor \log n\rfloor$.

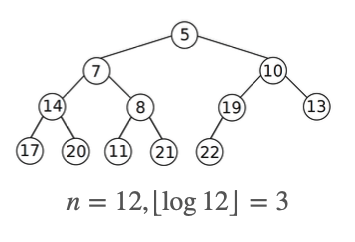
Quindi un heap ha almeno tanti nodi quandi ne ha un albero binario completo perfettamente bilanciato di altezza $h-1$. $n>2^{(h-1)+1}-1=2^h-1$

E ovviamente non ha più nodi di quandi ne ha un albero binario completo perfettamente bilanciato di altezza $h$ $n\le 2^{h+1}-1$

L’heap binario viene rappresentato come un array, dove vengono inserite le chiavi livello per livello da sinistra a destra.

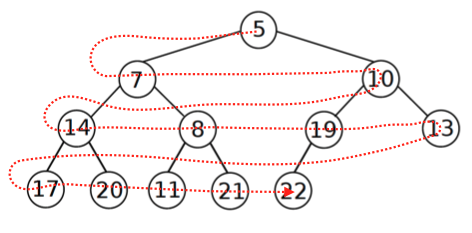
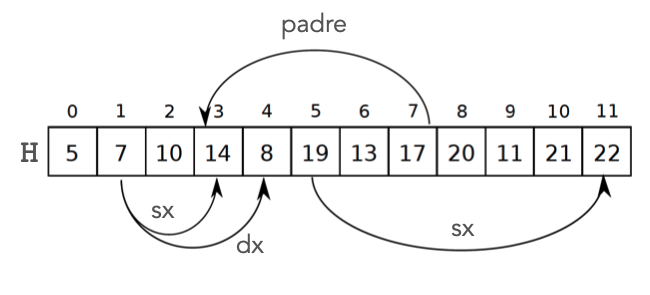
padre(i):
	return ⌈i/2⌉-1

figlioSinistro(i):
	return 2i+1

figlioDestro(i):
	return 2(i+1)

Primitive

1. costruisciHeap(H): costruisce un heap a partire da un array di chiavi memorizzate nell’array H - sarebbe $=(n\log n)$, ma facendo dei calcoli si scopre che è $O(n)$
2. minimoHeap(H) -> k: ritorna la chiave minima memorizzata in H - $O(1)$
3. decrementaChiaveHeap(H, i, k): decrementa il valore della chiave all’indice i nell’heap H, impostando il valore a k - $O(\log n)$
4. inserzioneChiaveHeap(H, k): inserisce una nuova chiave k in H - $O(\log n)$
5. heapify(H, i): ripristina la proprietà dell’ordinamento di un heap in seguito all’incremento di una chiave già presente nell’heap - $O(\log n)$
6. estrazioneMinimoHeap(H) -> k: restituisce la chiave minima e la elimina dell’heap - $O(\log n)$

minimoHeap(H):
		return H[0]

decrementaChiaveHeap(H, i, k):
	if H[i] < k then
		return error "Chiave maggiore di quella attuale"
	H[i] := k
	while i > 0 and H[padre(i)] > k do
		scambia H[padre(i)] con H[i]
		i := padre(i)

inserzioneChiave(H, k):
	if dim(H) == H.lenght then
		return error "L'heap è pieno"
	setDim(H) := dim(H) + 1
	H[dim(H)] := k
	decrementaChiaveHeap(H, dim(H), k)

heapify(H, i):
	min := i
	s := figlioSinistro(i)
	d := figlioDestro(i)

	if s <= dim(H) and H[s] < H[i] then
		min := s

	if d <= dim(H) and H[d] < H[min] then
		min := d

	if min != i then
		scambia H[i] con H[min]
		heapify(H, min)

estrazioneMinimo(H):
	if dim(H) < 0 then
		return error "heap empty"
	
	tmp := minimo(H)
	H[0] := H[dim(H)]
	setDim(H) := dim(H) - 1
	heapify(H, 0)
	return tmp

costruisciHeap(H):
	for i=padre(dim(H)) downto 0 do
		heapify(H, i)

asd_22