DAG

Grafo diretto aciclico (Direct acyclic graph).

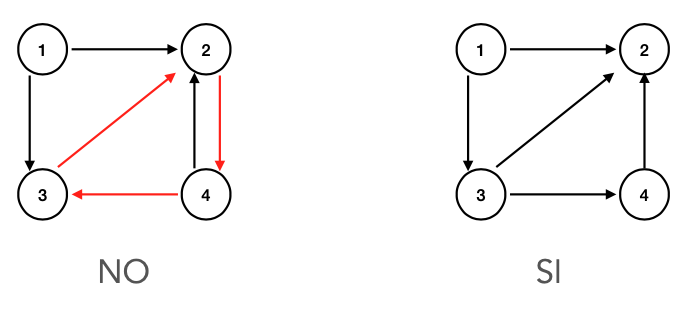
Nell’esempio corretto (quello di destra), il nodo 1 è un nodo sorgente, dal momento che non ha archi entranti, mentre il nodo 2 è un pozzo, perché non ha archi uscenti.

Ordinamento topologico

Dato un DAG G, un ordinamento topologico è un ordinamento lineare dei nodi tali che, se $(u,v)\in E$ allora u viene prima di v nell’ordinamento.

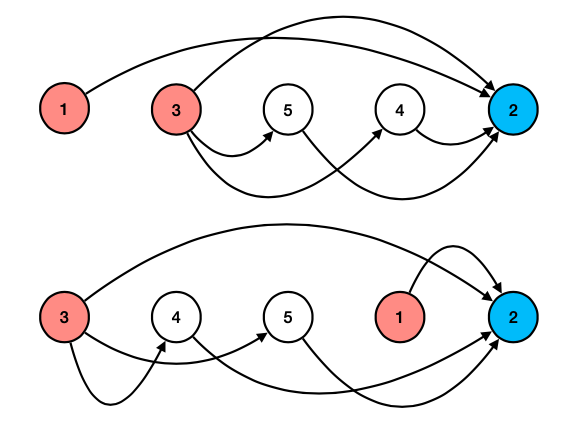
Gli archi sono diretti sempre da sinistra verso destra. NB: questo si può fare solo con un grafo aciclico.

Per arrivare ad un risultato del genere ci sono due modi:

• selezionare il nodo sorgente, inserirlo nell’ordinamento eliminandolo dal grafo, e continuare ricorsivamente. Calcolare il costo è complicato dal momento che cambia dall’implementazione del grafo.
• eseguire una DFS, e poi aggiungere all’ordinamento i nodi in base al valore di post, in ordine decrescente. Il costo è $O(|V|+|E|)$.

Ordinamento tramite DFS

In pratica non serve utilizzare post. Quando si finisce la visita di un nodo, si può aggiungere direttamente ad una pila.

TopologicalSort(G):
	s := new_stack()
	
	for all v ∈ V do
		visited[v] := false

	for all v ∈ V do
		if visited[v] == false then
			DFS_TS(G, v)
			push(s, v)
	return s

DFS_TS(G, v):
	visited[v] := true
	for all (v, u) ∈ E do
		if visited[u] == false then
			DFS_TS(G, u)

asd_28