Metodo di Gauss

• Eliminazione o fattorizzazione di Gauss
  • Passaggi
  • Pseudocodice
  • Costo
• Proprietà delle trasformazioni elementari di Gauss
• Unicità della fattorizzazione
• Fallimento dell’algoritmo
• Matrici simmetriche
  • Matrici simmetriche definite positive

Si ha sempre il sistema $Ax=b$. Il metodo di Gauss si divide in due fasi per la risoluzione:

1. Eliminazione o fattorizzazione di Gauss: si estraggono le matrici triangolare inferiore $L$ e superiore $U$ tali che $A=LU$
2. Costruzione e soluzione sistema triangolare equivalente a quello iniziale. Da $A=LU$ si ha un sistema 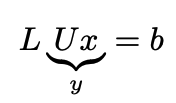$LUx=b\Rightarrow \{\begin{array}{l}Ly=b\\ Ux=y\end{array}$ Questa seconda fase prevede poi due diversi passi, ovvero la soluzione del sistema triangolare inferiore $Ly=b$ per sostuzione in avanti, e il sistema triangolare superiore $Ux=y$ per sostuzione all’indietro.

Eliminazione o fattorizzazione di Gauss

Ipotesi: A non singolare.

Fattorizzazione di Gauss

Dal momento che $L_{n-1}{L}_{n-2}...L_2{L}_{1}A=U$, si ha che quindi $A=L_1^{-1}{L}_2^{-1}...L_{n-1}^{-1}U$. Se si indica L con $L=L_1^{-1}{L}_2^{-1}...L_{n-1}^{-1}$, si ha in definitiva che $A=LU$. L è una matrice triangolare inferiore non singolare, dal momento che è il prodotto di matrici triangolari inferiori non singolari.

Per ogni passo, si ottiene una matrice $A_k$ con $k=1,...,n-1$ partendo da $A_1=A$. Il passo $k$ quindi ricava una matrice $A_{k+1}$ tramite combinazioni lineari delle righe di $A_k$, in modo che gli elementi sotto la diagonale principale siano nulli.

I passi sono $n-1$.

Passaggi

Si parte prendendo un elemento come pivot, ad esempio $a_{11}$ (che deve essere diverso da 0). Si calcolano i moltiplicatori, ovvero i valori che moltiplicati al pivot annullano gli elementi al di sotto. $m_{i1}=\frac{a_{i1}}{a_{11}}$, con $i=2,...,n$ Si ha quindi una combinazione lineare tra la riga i e la riga 1, con coefficiente $-m_{i1}$.

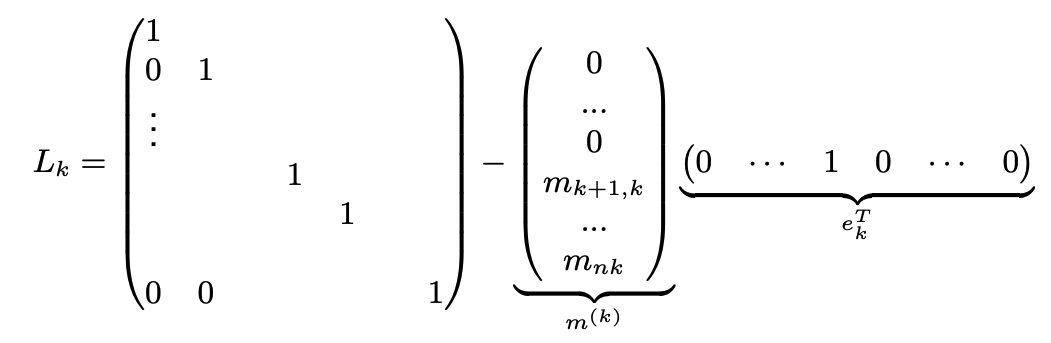
Al passo $k$ si ha questo. $A_{k+1}=L_k{A}_k$ La matrice $L_k$ è detta k-esima trasformazione elementare di Gauss, ed è definita in funzione dei moltiplicatori del k-esimo passo.

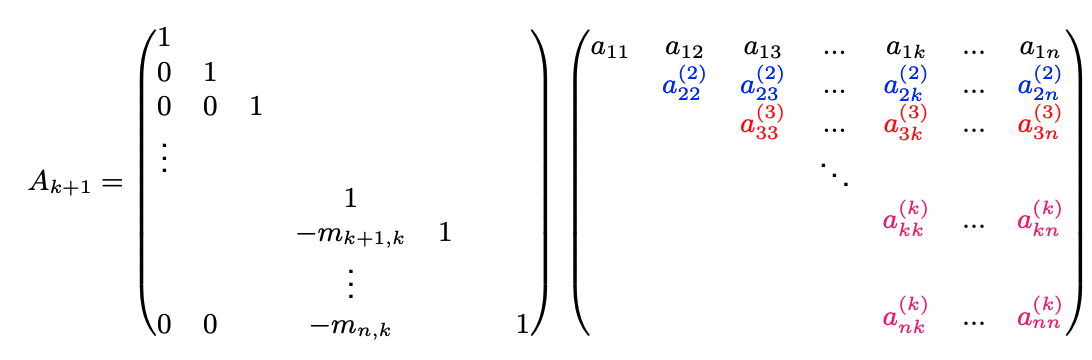
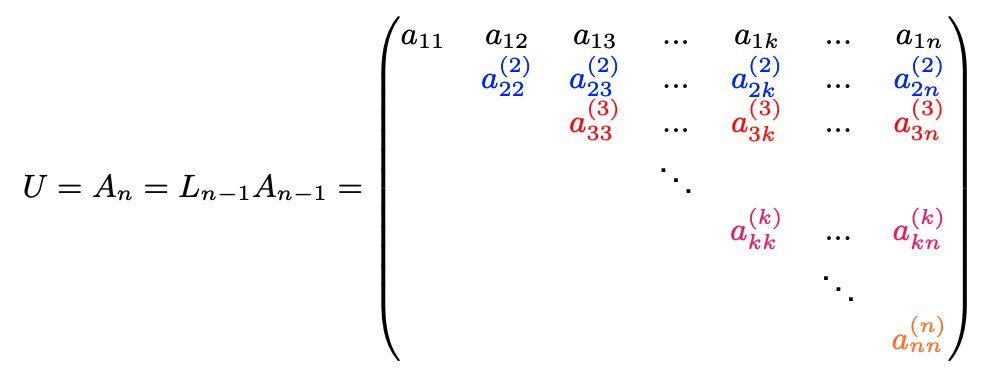
Dopo $n-1$ passi, si rimane con una matrice triangolare superiore $U$. Il procedimento di eliminazione equivale ad una successione di prodotti matriciali, $U=L_{n-1}{A}_{n-1}=L_{n-1}{L}_{n-2}{A}_{n-2}=...=L_{n-1}{L}_{n-2}...L_{2}L-1A$.

Attenzione

Tutto questo è ben posto se e solo se $a_{kk}^{(k)}\ne 0$.

Per aggiornare un elemento, si esegue:

$$a_{ij}^{(k+1)}=a_{ij}^{(k)}-a_{kj}^{(k)}\times (\frac{a_{ik}^{(k)}}{a_{kk}^{(k)}}),\text{ con }k=1,...,n-1\text{, e }i,j=k+1,...,n$$

Pseudocodice

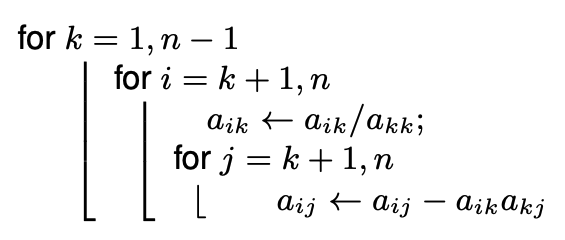
Applicato l’algoritmo, si ha una matrice di questo tipo:

$$\left(\begin{array}{cccccc}{a}_{11}& a_{12}& a_{13}& ...& ...& a_{1n}\\ m_{21}& a_{22}^{(2)}& a_{23}^{(2)}& ...& ...& a_{2n}^{(2)}\\ m_{31}& m_{32}& a_{33}^{(3)}& ...& ...& a_{3n}^{(3)}\\ ...& ...& ...& ...& ...& ...\\ m_{i1}& m_{i2}& ...& a_{ii}^{(i)}& ...& a_{in}^{(i)}\\ m_{n1}& m_{n2}& ...& m_{ni}& m_{n,n-1}& a_{nn}^{(n)}\end{array}\right)$$

Costo

Somme e prodotto: $O(\frac{n^3}{3})$ Quozienti: $O(\frac{n^2}{2})$

Proprietà delle trasformazioni elementari di Gauss

$$L_k=\left(\begin{array}{cccccc}1& & & & & \\ 0& 1& & & & \\ ...& & & & & \\ 0& 0& ...& 1& & \\ 0& 0& ...& -m_{k+1},k& 1& \\ 0& 0& ...& -m_n,k& & 1\end{array}\right)$$

$L_k$ è triangolare con diagonale unitaria, quindi il determinante è $det(L_k)=1$, quindi la matrice è non singolare.

Si può quindi riassumere con $L_k=I-m^{(k)}{e}_k^T$, dove $e_k$ è un vettore dove tutti gli elementi sono 0, a parte l’elemento k. Essendo trasposto, diventa vettore riga.

L’inversa di questa matrice, ovvero $L_k^{-1}$, è data da $L_k=I+m^{(k)}{e}_k^T$, dove in pratica cambia solo il segno di sottrazione.

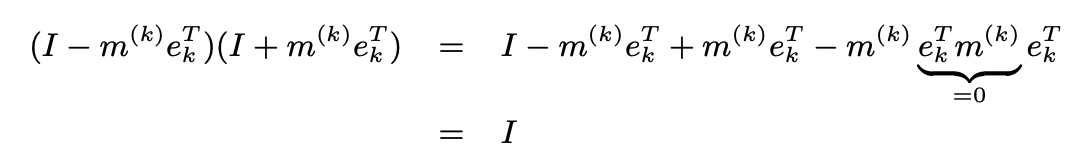
Osservazione

Uguaglianza dei determinanti: $a_{11}{a}_{22}^{(2)}...a_{kk}^{(k)}=1\ast A^{(k)}$, dove $A^{(k)}$ è il k-esimo minore principale di A, ovvero il determinante della sottomatrice formata delle prime k righe e k colonne.

Condizione necessaria e sufficiente

affinchè tutti i pivot siano non nulli, e quindi si possa compiere la fattorizzazione, è che tutti i minori principali di A siano diversi da zero, eccetto al massimo l’ultimo, ovvero se $det(A)=0$, si può comunque portare a termine.

Unicità della fattorizzazione

Nell’ipotesi che A sia non singolare, allora $A=LU$ è unica.

Dimostrazione

Supponiamo che esistano due coppie $A=L_1{U}_1$ e $A=L_2{U}_2$. $L_1$ e $L_2$ sono non singolari. Se $A$ è non singolare, allora anche $U_1$ e $U_2$ devono essere non singolari. Quindi si ha che $L_1{U}_1=L_2{U}_2\Rightarrow L_1^{-1}{L}_2=U_1{L}_2^{-1}$. $L_1^{-1}{L}_2$ è triangolare inferiore, e $U_1{L}_2^{-1}$ è triangolare superiore. Dal momento che sono eguagliate, si ha che devono essere matrici diagonali. Ma dal momento che $L_1^{-1}{L}_2$ ha diagonale unitaria, l’unica soluzione è $I$.

Fallimento dell’algoritmo

Non tutte le matrici invertibili hanno tutti i minori principali diversi da zero ($\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right)$). Per convenire a questi errori, si utilizzano alcune modifiche del metodo di Gauss, come ad esempio:

• Strategie di pivoting

Matrici simmetriche

Per le matrici simmetriche si utilizza il Fattorizzazione matrici simmetriche. La risoluzione del sistema tramite $LD{L}^T$ si fa:

$$Ax=b\iff L\underset{=z}{\underbrace{D{L}^{T}x}}=b$$ $$\{\begin{array}{ll}Lz=& b\\ Dy=& z\\ L^{T}x=& y\end{array}$$

Attenzione

Il vettore $y$ si calcola con l’algoritmo di soluzione dei sistemi diagonali:

$$y_i=\frac{z_i}{d_{i}i},i=1,...,n$$

Matrici simmetriche definite positive

Godono delle seguenti proprietà:

• tutti i minori principali sono positivi
• tutti gli autovalori sono reali positivi
• $x^{T}Ax\ge 0\forall x\in {\mathbb{R}}^n$ e $x^{T}Ax=0\iff x=0$