Algoritmi di programmazione dinamica

Anche in questo caso, come per gli algoritmi greedy, la programmazione dinamica può essere applicata solo se il problema ha sottostruttura ottima.

Se non si sa quali sottoproblemi risolvere, risolvere tutti i sottoproblemi e conservare i risultati ottenuti per utilizzarli successivamente nel risolvere il problema di dimensione maggiore.

Input: DAG G=(V, E), nodo sorgente s, funzione sugli archi $c:E\to R$ Output: distanze minime dei nodi di G da s

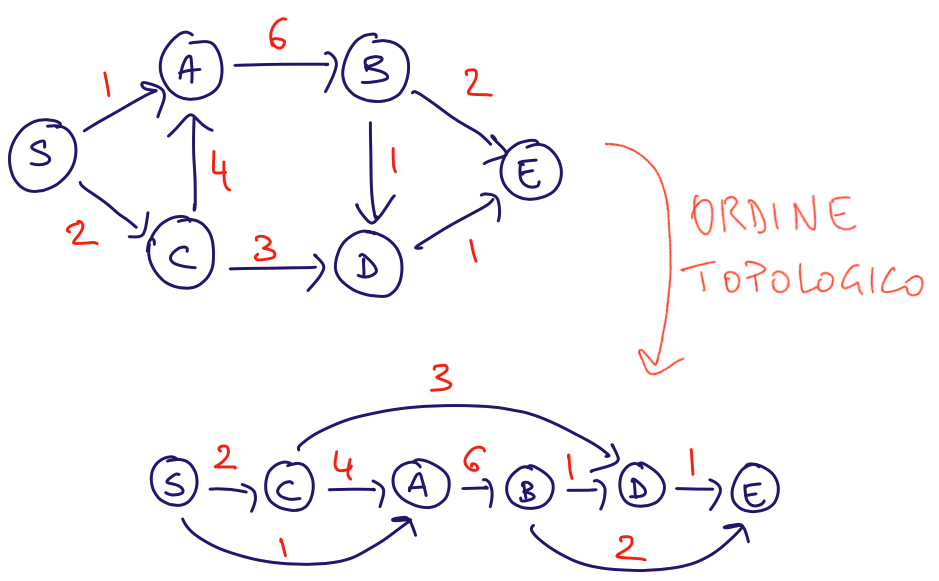
Il nodo D può essere raggiunto solo da C e B. Se calcolo quindi la distanza minima di C e di B dalla sorgente, posso calcolare la distanza minima per D sempre dalla sorgente.

$$dist[D]=min\begin{array}{c}\{\begin{array}{l}dist[C]+3\\ dist[B]+1\end{array}\end{array}$$

In questo caso ci sono $|V|$ sottoproblemi, uno per ogni nodo. Per trovare la distanza minima di un nodo v dalla sorgente, si compongono i sottoproblemi relativi ai nodi che hanno un arco diretto verso v. Per fare ciò, serve l’ordine topologico del DAG.

shortest_path(G, c, s):
	TS := topological_sort(G) # restituisce una pila
	
	for all v in V do
		dist[v] := +∞
	dist[s] := 0
	v := pop(TS)

	while v != s do
		v := pop(TS)

	while not is_empty(TS) do
		dist[v] := min((u, v) in E){dist[u] + c(u, v)} 
		# il minimo di tutti gli archi che da un nodo qualsiasi u vanno in v
		
		v := pop(TS)
	return dist[]

Un altro esempio può essere trovare la sottosequenza crescente più lunga in un array. Input: sequenza di n numeri $A=<a_1,a_2,...,a_n>$ Output: sottosequenza crescente più lunga in A

title: Definizione
Data una sequenza di elementi $A=<a_1, a_2, ..., a_n>$ e dato un insieme $k \in [1...n]$ indici $I=\{i_1, i_2, ..., i_k\} \subseteq \{1, 2, ..., n\}$ tale che $1 \le i_1 \le i_2 \le... \le i_k \le n$, la sequenza $A'=<a_{i_1}, a_{i_2}, ..., a_{i_n}>$ è una sottosequenza di A.

Si può implementare un algoritmo in cui si va a cercare il cammino più lungo in un DAG. Il DAG si costruisce mappando gli elementi della sequenza in nodi, che vengono ordinati secondo l’ordine iniziale. A questo punto si aggiungono gli archi tra $a_i$ e $a_j$, solo se $a_i\le a_j$.

Come sottoproblema si può vedere $L[j]$ come lunghezza del cammino più lungo che termina in $j$.

Si può calcolare $L[j]$ in funzione delle soluzioni dei sottoproblemi più piccoli, ovvero con $L[i],i<j$. $L[j]={\max }_{(i,j)\in E}\{L[i]\}+1$

Per questo algoritmo si può utilizzare la ricorsione. Per calcolare $L[k]$ sono necessarie $2^{k-1}$ chiamate ricorsive, il che rende tutto di costo esponenziale.

Per questo, si evita la ricorsione, e si passa all’iterazione. In questo modo si possono salvare i valori già calcolati, senza doverli ricalcolare di nuovo.

LSI(A):
	costruire il DAG di G a partire da A
	for j = 1 to n do
		L[j] := 1
	for j = 2 to n do
		L[j] = max((i, j) in E) {L[i]} + 1
	return max_j L[j]

Problema dello zaino All Pairs Shortest Paths

asd_38