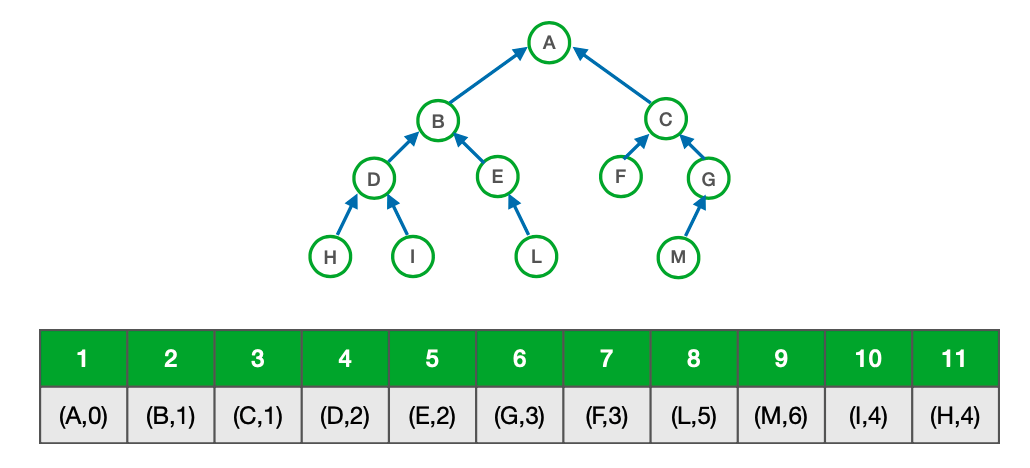
Alberi generici

Negli alberi generici ogni nodo dell’albero può avere un numero qualunque di figli.

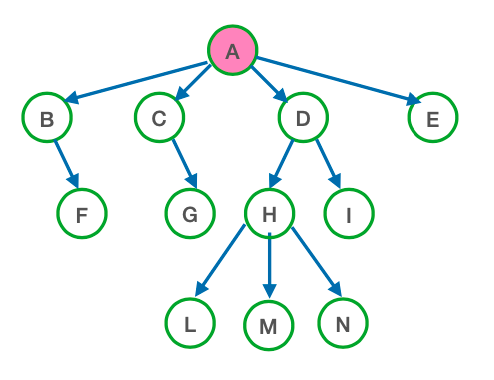
Visita in profondità

Molto simile alla visita in profondità per gli Visita in profondità - DFS. In questo caso si modifica leggermente la parte finale del metodo, dal momento che i figli non sono più massimo due.

DFS_pre_order(L):
	if L != nil then
		print(L.val)
		for all e ∈ children(L) do
			DFS_pre_visit(e)

Chiamata principale: DFS_pre_order(L), dove L è la radice dell’albero.

DFS_post_order(L):
	if L != nil then
		for all e ∈ children(L) do
			DFS_pre_visit(e)
		print(L.val)

Chiamata principale: DFS_post_order(L), dove L è la radice dell’albero.

La versione in-order in questo caso non è possibile perchè non non ci sono solo due figli.

Visita in ampiezza

Molto simile alla visita in profondità per gli Visita in ampiezza - BFS.

BFS(L):
	if L != nil then
		q := new_queue()
		enqueue(q, L)
		while !is_empty_list(q) do
			e := dequeue(q)
			print(e.val)
			for all u in children(e) do
				enqueue(q, u)

Creazione degli alberi generici

Ci sono diversi modi per creare un albero:

• vettore dei figli
• primo figlio e fratello successivo
• vettore dei padri

Vettore dei figli

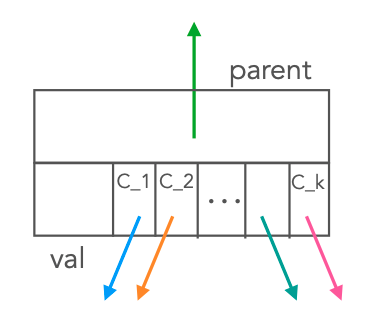
Ogni nodo ha:

• un puntatore al nodo padre
• un valore
• n campi per gli n possibili figli

Dato che si deve allocare spazio in memoria per i possibili n figli anche se magari ce ne è nemmeno uno, c’è un grosso possibile spreco di memoria.

Primo figlio e fratello successivo

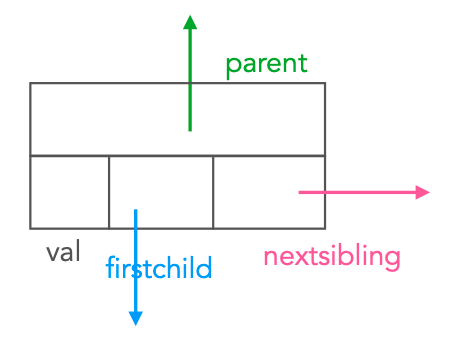
Ogni nodo ha:

• un puntatore al primo figlio
• un puntatore al primo fratello
• un puntatore al nodo padre
• un valore

Vettore dei padri

I nodi in questo caso sono memorizzati in un array di coppie, dove ogni coppia contiene il valore memorizzato nel nodo e l’indice dell’array che contiene il nodo padre (val, p).

asd_21