Sistemi lineari

Data una matrice $A\in {\mathbb{R}}^{n\times n}$ detta matrice dei coefficienti, con termine noto $b\in {\mathbb{R}}^n$:

$$A=\left(\begin{array}{cccc}{a}_{11}& a_{12}& ...& a_{1n}\\ a_{21}& a_{22}& ...& a_{2n}\\ ...& ...& ...& ...\\ a_{n1}& a_{n2}& ...& a_{nn}\end{array}\right)b=\left(\begin{array}{c}{b}_1\\ b_2\\ ...\\ b_n\end{array}\right)$$

Il risultato è il vettore $x$ che soddisfa $Ax=b$

In forma esplicita si ha:

$$\{\begin{array}{llc}{a}_{11}{x}_1+a_{12}{x}_2+...+a_{1n}{x}_n& =& b1\\ a_{21}{x}_1+a_{22}{x}_2+...+a_{2n}{x}_n& =& b2\\ ...& & \\ a_{n1}{x}_1+a_{n2}{x}_2+...+a_{nn}{x}_n& =& bn\end{array}$$

Definizione

Una matrice $A\in {\mathbb{R}}^{n\times n}$ si dice non singolare (o invertibile) se esiste una matrice $X$ tale che $AX=XA=I$; la matrice $X$ si dice inversa di $A$ e si indica $X=A^{-1}$.

Teorema di Rouché-Capelli

Se una matrice $A$ è non singolare, allora esiste una unica soluzione del sistema lineare $Ax=b$.

Sistema mal condizionato

Un sistema è mal condizionato quando le righe del sistema sono quasi linearmente dipendenti.

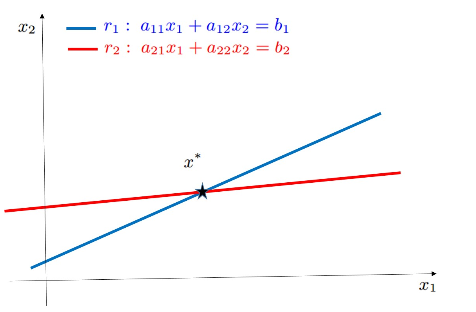
In un sistema ben condizionato, con $n=2$, si ha che il punto trovato è il punto di intersezione.

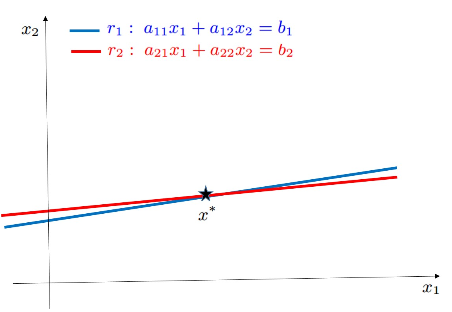
In un sistema mal condizionato, si ha che $r_1$ e $r_2$ sono quasi coincidenti: Per avere una rappresentazione più visuale del perchè l’errore è malcondizionato, abbiamo:

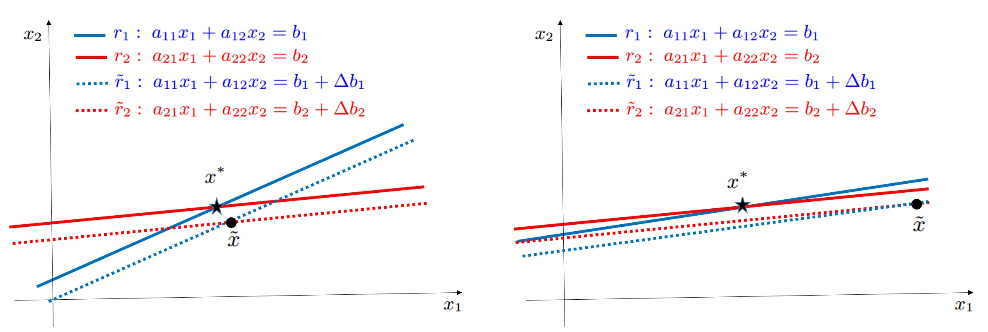
Che relazione c’è quindi tra l’errore relativo sulle soluzioni e l’errore relativo sui dati?

$$\frac{||x\ast -\tilde{x}||}{||x\ast ||}=[?]\frac{||\Delta b||}{||b||}$$

Viene in campo l’Indice di condizionamento di una matrice.

Stima dell’errore inerente nella soluzione di un sistema

$x\ast$ soluzione del sistema di dati $(A,b)$. $\tilde{x}$ soluzione del sistema di dati perturbati $(A+\Delta A,b+\Delta b)$. $e_A=\frac{||\Delta A||}{||A||},e_b=\frac{||\Delta b||}{||b||}$ errori relativi presenti nei dati.

Si può dimostrare che l’errore relativo inerente $e(\tilde{x})=\frac{||x\ast -\tilde{x}||}{||x\ast ||}$ soddisfa: $e(\tilde{x})\le \frac{k(A)}{1-k(A)e_A}(e_A+e_b)$

Risoluzione sistemi lineari

Ecco alcuni metodi per la risoluzione dei sistemi lineari.

Attenzione!

Il teorema di Rouché-Capelli, che implicitamente suggerisce un algoritmo per il calcolo di $x=A^{-1}b$, non è una valida alternativa per l’elevato costo computazionale e la stabilità.

Esistono due tipi di algoritmi per risolvere i sistemi:

• algoritmi diretti: numero finito di operazioni
• algoritmi iterativi: successione di vettori che all’infinito si avvicina alla soluzione del sistema

Algoritmi diretti

Sistemi facili

Sistemi diagonali

Sistemi triangolari