Binary search

Input sequenza ordinata di n elementi memorizzata in un array L dove $L[0]\le L[1]\le ...\le L[n-2]\le L[n-1]$

Un elemento key dello stesso tipo degli elementi in $L$.

Output Posizione di key in $L$, se key sta in $L$, -1 altrimenti.

Esempio: $L=<1,3,4,6,7,8,23,56,78,89,125,136>$ key = 8 output = 5

Con key = 13 si ha un output = -1.

Soluzione non ottimale

Una soluzione non ottimale è quella di andare a confrontare uno per uno tutti gli elementi dell’array. Nel caso peggiore però si confrontano tutti gli elementi, quindi il costo computazionale è un $O(n)$. Si può fare di meglio.

Soluzione ottimale

La soluzione ottimale è appunto la binary search.

1. confrontare la key con l’elemento centrale dell’array
2. se l’elemento e la key sono uguali, allora ritorno la posizione
3. se l’elemento è minore della key, scarto tutta la parte sinistra dell’array e ricomincio l’algoritmo nella parte destra
4. se l’elemento è maggiore della key, scarto la parte sinistra e ricomincio l’algoritmo nella parte sinistra
5. se non ci sono più elementi tra cui cercare mi fermo e ritorno -1

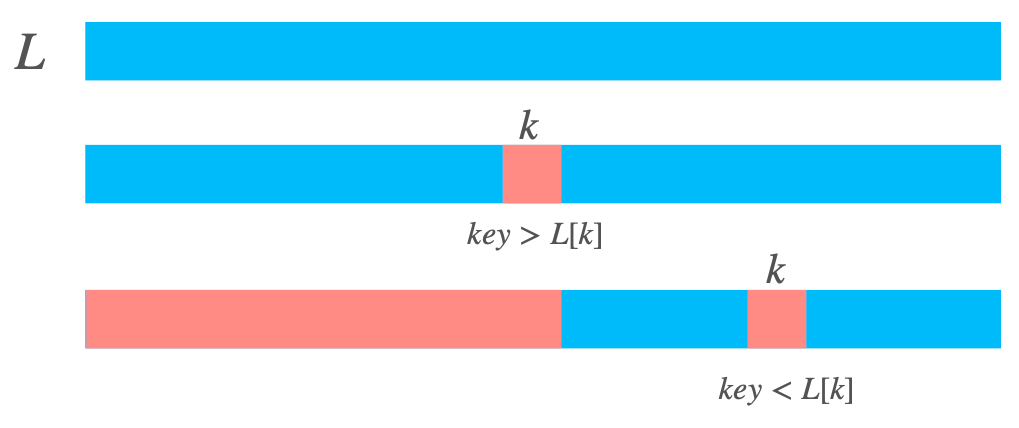
L’indice $k$ si calcola sommando i due estremi $i$ e $j$, e dividendo per 2. Per avere un elemento intero, si prende sempre la parte inferiore/superiore. $k=\lfloor \frac{i+j}{2}\rfloor$

BinarySearch(L, n, key):
	i := 0
	j := n-1
	while i <= j:
		k := ⎣(i+j)/2⎦
		
		if L[k] == key then
			return k
		else if L[k] < key then
			i := k + 1
		else
			j := k - 1

	return -1

Il caso peggiore è quando la key non è presente. Quante volte viene ripetuto il ciclo while nel caso peggiore?

$\#it(n)\le \log n+1$, dove $\#it(n)$ è il numero di iterazioni necessarie nel caso peggiore.

La dimostrazione si fa per induzione: Caso base $n=1\to \#it(1)=1\le 1=\log 1+1$

Passo induttivo $\forall k=1,...,n-1:\#it(k)\le \log k+1$

Con $n$ dispari si ha $\frac{n-1}{2}=\frac{n}{2}-\frac{1}{2}=\lfloor \frac{n}{2}\rfloor$ Con $n$ pari si ha invece la parte sinistra che conta $\frac{n}{2}-1\le \lfloor \frac{n}{2}\rfloor$ elementi, mentre la parte destra ne conta esattamente $\lfloor \frac{n}{2}\rfloor$.

In entrambi i casi si ha che $\#it(n)\le 1+\#it(\lfloor \frac{n}{2}\rfloor )$. Quindi, dall’ipotesi induttiva \begin{align}\#it(n) \le 1+\#it(\lfloor\frac{n}2\rfloor) & \le 1 + \log(\lfloor\frac{n}2\rfloor) + 1 \\ & \le 1 + \log(\frac{n}2) + 1 \\ & \le 1+\log n - \log 2 + 1 = 1+\log n\end{align}

In finale, il costo computazionale della binary search è logaritmico $O(\log n)$.

Versione ricorsiva

BinarySearch(L, i, j, key):
	if j-i < 0 then
		return -1
	else
		k := ⎣(i+j)/2⎦
		if L[k] == key then
			return k
		else if L[k] < key then
			return BinarySearch(L, k + 1, j, key)
		else
			return BinarySearch(L, k, k - 1, key)

Usando la ricorsione, si deve specificare anche la chiamata principale: BinarySearch(L, 0, n-1, key)

asd_09