Trasformata di Fourier

Ogni funzione periodica può essere decomposta in somme di seni e coseni.

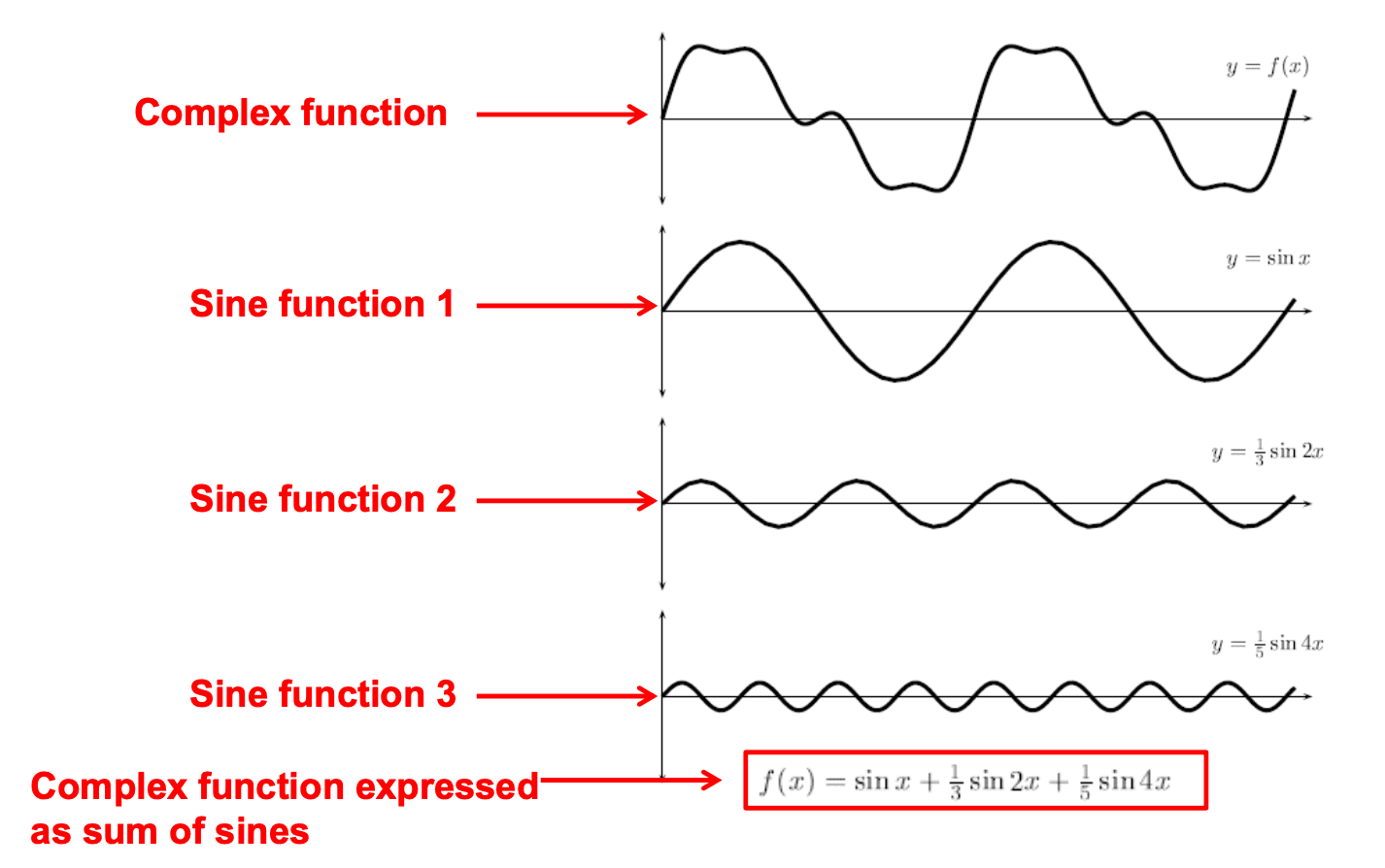
Dal momento che è matematicamente più semplice analizzare gli effetti di trasformazioni, rumore ecc su funzioni seno semplici, per poi unirli ed avere l’effetto della funzione complessa iniziale.

NOTA: le funzioni seno dell’immagine sopra hanno frequenze differenti, e queste frequenze sono multipli tra di loro. Sono quindi chiamate armoniche.

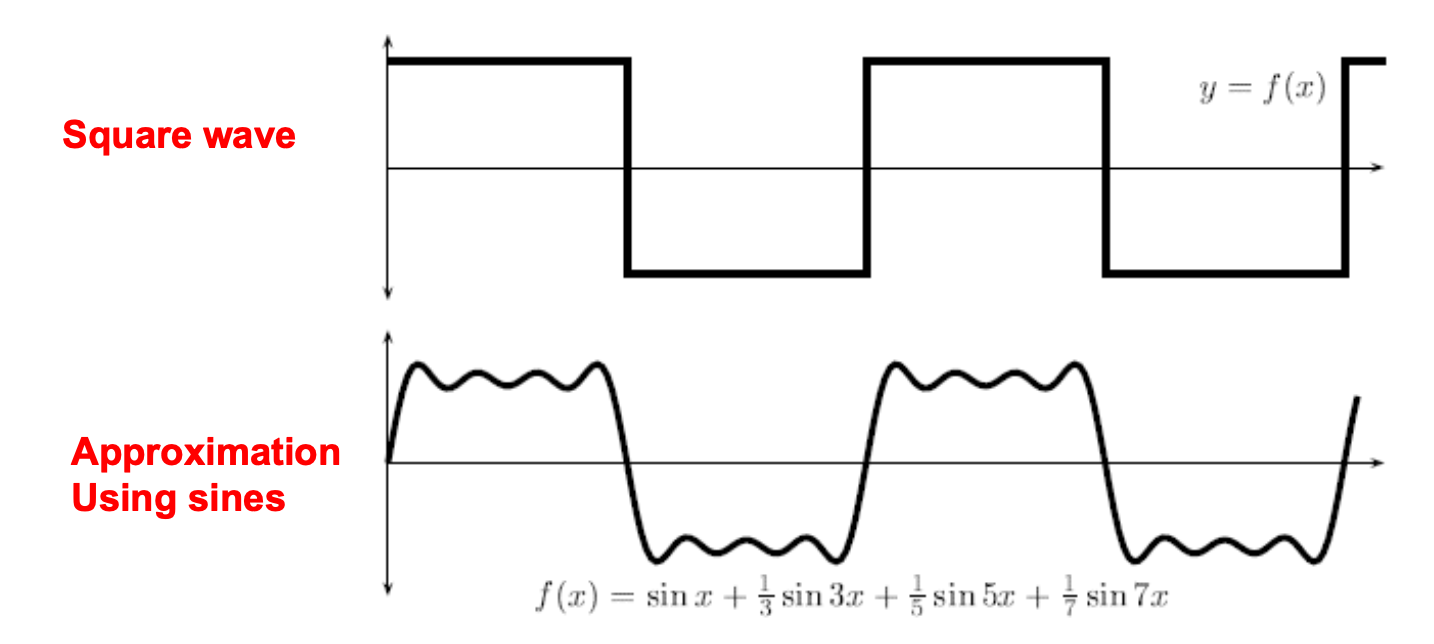
I seno vanno ad infinito. Più funzioni seno si aggiungono, più ci si avvicina all’approssimazione della funzione di partenza.

Tecniche spettrali

Tecnica di rappresentazione e analisi di segnali in domini di frequenza che includono audio, immagini e video. Si decompongono i segnali come somma di una serie di funzioni seno e coseno (funzioni armoniche). Queste tecniche possono migliorare l’efficienza dell’image processing, come ad esempio effetti, concetti e tecniche.

Queste tecniche includono trasformata di Fourier, trasformata discreta di Fourier e la trasformata discreta del coseno.

Funzioni periodiche

$f(x)=cos(x)$ Una funzione si dice periodica se: $cos(x)=cos(x+2\pi )=cos(x+4\pi )=...=cos(x+k2\pi )$

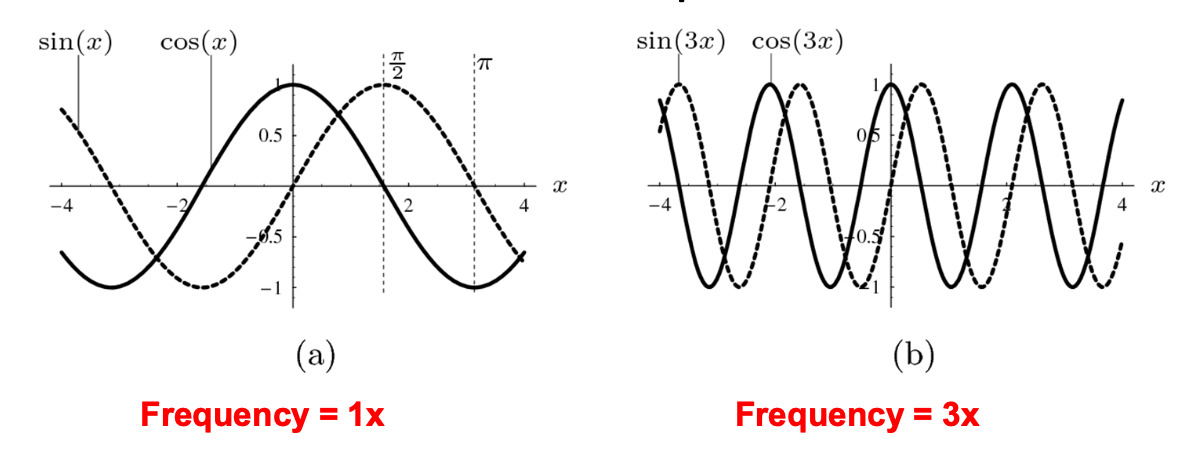
La relazione tra il periodo T, la frequenza $f$ e la velocità angolare $\omega$ è: $f=\frac{1}{T}=\frac{\omega }{2\pi }\text{mbox}cheequivalea\omega =2\pi f$

$\sin (\omega x)=\cos (\omega x-\frac{\pi }{2})$

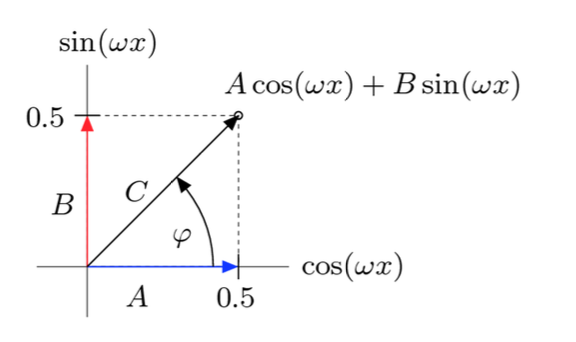
La somma di seno e coseno con stessa frequenza ma diversa ampiezza crea un nuovo sinusoide. $A\cdot \cos (\omega x)+B\cdot \sin (\omega x)=C\cdot \cos (\omega x-\phi )$

L’ampiezza e l’angolo di C si calcolano come: $C=\sqrt{A^2+B^2}$ e $\phi ={\tan }^{-1}(\frac{B}{A})$

Norazione numeri complessi di Eulero $z=e^{i\Theta }=\cos (\Theta )+i\cdot \sin (\Theta )$

Combinare seno e coseno con stessa frequenza: $e^{i\Theta }=e^{i\omega x}=\cos (\omega x)+i\cdot \sin (\omega x)$

Quindi quasi ogni funzione periodica g(x) con frequenza fondamentale ${\omega }_0$ può essere descritta come somma di sinusoidi $g(x)={\sum }_{k=0}^{\infty }[A_k\cos (k{\omega }_{0}x)+B_k\sin (k{\omega }_{0}x)]$ Serie di Fourier $A_k$ e $B_k$ sono chiamati coefficienti di Fourier.

Integrale di Fourier

Per funzioni non periodiche, si utilizza l’integrale di Fourier. $g(x)={\int }_0^{\infty }{A}_{\omega }\cos (\omega x)+G_{\omega }\sin (\omega x)d\omega$ con i coefficienti che si possono calcolare tramite: $A_{\omega }=A(\omega )=\frac{1}{\pi }{\int }_{-\infty }^{\infty }g(x)\cdot \cos (\omega x)dx$ $B_{\omega }=B(\omega )=\frac{1}{\pi }{\int }_{-\infty }^{\infty }g(x)\cdot \sin (\omega x)dx$

Trasformata di Fourier

Transizione di una funzione $g(x)$ al suo spettro di Fourier $G(\omega )$

& = \frac{1}{\sqrt{2\pi}} \int^{\infty}_{-\infty}g(x)\cdot e^{-i\omega x} dx\end{align}$$ ## Trasformata di Fourier inversa $$\begin{align}g(x) & = \frac{1}{\sqrt{2\pi}} \int^{\infty}_{-\infty}G(\omega)\cdot[\cos(\omega x)-i\cdot \sin(\omega x)]d\omega \\ & = \frac{1}{\sqrt{2\pi}} \int^{\infty}_{-\infty}G(\omega)\cdot e^{i\omega x} d\omega\end{align}$$ #sva_s10