Visite ai grafi

Esistono anche per i grafi, come per alberi, due tipi di visita:

• Visita in profondità (DFS)
• Visita in ampiezza (BFS)

Gli archi possono assumere significati diversi, quando si esegue una visita. Esiste infatti una classificazione archi.

Visita in profondità

Usa la ricorsione e costa $O(|V|+|E|)$.

Molto simile alla DFS per gli alberi binari. Anche qui esistono le versioni pre e post-order, e dopo la visita ad un nodo si cerca di allontanarsi sempre di più. Si visitano tutti i nodi del grafo anche se ci sono più componenti.

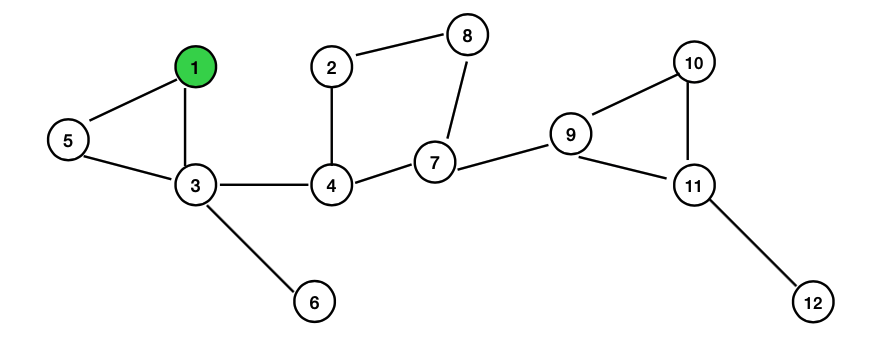
La visita genera un albero, chiamato albero di copertura, che può essere salvato per visitare nuovamente più velocemente.

Per eseguire una DFS serve avere un array visited grande quando il numero di nodi nel grafo.

DFS(G):
	for all v ∈ V do
		visited[v] := false
		[prev[v] := 0]
	for all v ∈ V do
		if visited[v] == false then
			DFS_visit(G, v)

DFS_visit(G, v):
	visited[v] := true
	esamina nodo (pre-visit)
	for all (v, u) ∈ E do
		if visited[u] == false then
			[prev[u] := v]
			DFS_visit(G, u)
	esamina nodo (post-visit)

Il costo computazionale è $O(|V|+|E|)$.

Tra parentesi quadre si può trovare prev[v] := 0. In questo caso si usa un array per tenere traccia di quale nodo si è utilizzato per trovarne un’altro. Questo è usato per creare la foresta di copertura. Dove prev[v] = 0, si ha che è una radice di un albero di copertura.

Ricerca di un ciclo in un grafo

**Test grafo aciclico**
*Input*
grafo $G=(V, E)$
 
*Output*
`true` se il grafo G contiene un ciclo, false altrimenti.

Per un grafo non orientato si ha:

DFS(G):
	for all v ∈ V do
		visited[v] := false
		[prev[v] := 0]
	for all v ∈ V do
		if visited[v] == false and DFS_visit(G, v) then
			return true
	return false

DFS_visit(G):
	visited[v] := true
	for all (v, u) ∈ E do
		if visited[u] == true or DFS_visit(G, u) then
			return true
	return false

Un grafo orientato, invece, ha un ciclo se e solo se c’è un arco qualificato come back edge in una visita DFS. Per questo si utilizza un DAG.

Le applicazioni della DFS possono essere:

• foresta/albero di copertura
• ricerca cicli nel grafo
• connettività

Visita in ampiezza

Utilizza una coda e costa $O(|V|+|E|)$.

Molto simile alla BFS per gli alberi binari. Si visita un nodo, i suoi vicini, i vicini dei vicini ecc… Si visitano tutti i nodi raggiungibili da un nodo sorgente.

title: Attenzione
In un grafo diretto, se un nodo non è raggiungibile attraverso il nodo sorgente che si sceglie, non sarà mai raggiungibile.

BFS(G, s):
	for all u ∈ V do
		visited[u] := false
	visited[s] := true
	q := new_queue()
	enqueue(q, s)
	
	while not is_empty_queue(q) do
		u := dequeue(q)
		for all (u, v) ∈ E do
			if visited[v] == false then
				enqueue(q, v)
				visited[v] := true

Il codice precedente si può modificare in modo da avere un array per le distanze dalla radice

BFS(G, s):
	for all u ∈ V do
		dist[u] := +∞
		prev[u] := 0
	prev[s] := 0
	q := new_queue()
	enqueue(q, s)
	
	while not is_empty_queue(q) do
		u := dequeue(q)
		for all (u, v) ∈ E do
			if dist[v] == +∞ then
				enqueue(q, v)
				prev[v] := u
				dist[v] := dist[u] + 1

Il costo di questo algoritmo è di $O(|V|+|E|)$

I nodi durante l’esecuzione dell’algoritmo si dividono in:

• Mondo fermo: nodi già visitati e vicini esplorati (dist[.] < d)
• Frontiera: nodi già scoperti ma vicini non esplorati. Sono quelli contenuti nella coda (d <= dist[.] <= d+1)
• Mondo lontano: nodi non visitati (dist[.] = +∞)

???? cosa è questa storia????

asd_25asd_26asd_30