Merge sort

Il merge sort fa parte degli algoritmi di sorting. $\in O(n\log n)$

Input Sequenza di $n$ valori $A=<a_0,a_1,...,a_{n-1}>$.

Output Permutazione $<a_0^{\prime },a_1^{\prime },...,a_{n-1}^{\prime }>$ della sequenza $A$ tale che $a_0^{\prime }\le a_1^{\prime }\le ...\le a_{n-1}^{\prime }$

title: Attenzione
Come costo computazionale calcoliamo i confronti eseguiti tra i valori di A.

Questo algoritmo utilizza la tecnica Dividi et impera.

1. Dividi: dividi l’array in due parti uguali
2. Impera: ordina ogni array (quando c’è solo un elemento è già ordinato)
3. Combina/merge: fondi le due metà ordinando gli elementi

MergeSort(A, i, j):
	if i < j then
		k := ⎣(i+j)/2⎦
		MergeSort(A, i, k)
		MergeSort(A, k+1, j)
		Merge(A, i, k, j)

Chiamata principale: MergeSort(A, 0, n-1)

Nello pseudo codice appena scritto si richiama una procedura dal nome Merge. Questa prende in input due porzioni ordinate dell’array A, e ne fa il merge ordinato.

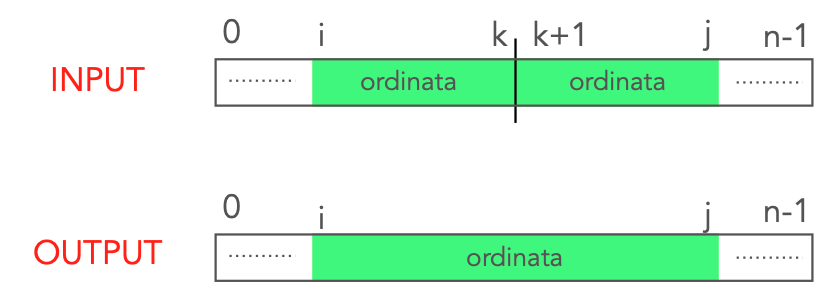
Merge(A, i, k, j):
	l := i
	r := k + 1
	t := 0
	B := [0..j-i] nuovo array
	while l <= k AND r <= j do
		if A[l] <= A[r] then
			B[t] := A[l]
			l := l + 1
		else 
			B[t] := A[r]
			r := r + 1
		t := t + 1

	// se la parte sinistra ha degli elementi ancora, si devono spostare
	// se è la parte destra ad averli, si può fare a meno perchè verranno
	// spostati dopo
	r := j
	for h = k downto l do
		A[r] := A[h]
		r := r - 1

	// copio tutto il contenuto di B in A
	for h = i to t + i - 1 do
		A[i] := B[h-i]

Il while viene ripetuto $O(j-i)$ volte, perchè si deve fare per tutti gli elementi. La copia viene eseguita su tutti gli elementi, quindi si ha un $\Theta (n)$.

Utilizzando il master theorem per calcolare il costo computazionale di Merge, si ha:

$$T(n)=\begin{array}{c}\{\begin{array}{ll}\Theta (1)& \text{mbox}sen=1\\ 2\cdot T(\frac{n}{2})+O(n)& \text{mbox}altrimenti\end{array}\end{array}$$

con $d=1,b=2,a=2$ si ha ${\log }_{2}2=1=d$, quindi il costo computazionale è di $O(n^{{\log }_{b}a}\log n)=O(n\log n)$

Nessuno tra gli [[algoritmi di sorting]] che risolve il problema utilizzando confronti tra elementi può fare meglio di $O(n\log n)$. Si ha che quindi per un algoritmo di ordinamento, il lower bound è $\Omega(n\log n)$.

Miglioramenti

Dal momento che si utilizza anche un $O(n)$ di spazio, e si fanno molte chiamate ricorsive, si può migliorare ulteriormente la velocità usando l’Insertion sort per il caso base (che diventa $s>1$), e per il resto continuare come sopra.

asd_13