Grafi
I grafi sono composti da nodi e archi.
, dove V è l’insieme di vertici, e E è l’insieme degli archi.
Esistono due tipi di grafi:
-
grafo diretto (orientato)
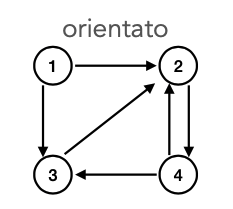Le coppie di E sono ordinate.
Il nodo v è adiacente al nodo u se esiste la coppia orientata (v, u). L’arco(u, v)è incidente in u e v, è uscente da u ed è entrante in v. -
grafo non diretto (non orientato)
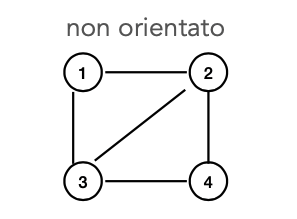Le coppie in E non sono ordinate.
Il nodo v è adiacente al nodo u se esiste la coppia (u, v). L’arco(u, v)è incidente in u e v.
Il grado (deg(v)) di un nodo è il numero di archi adiacenti a quel nodo. In un grafo orientato si parla di grado entrante e di grado uscente.
Il cammino è la sequenda di nodi tale che per .
La lunghezza del cammino è il numero di archi, e quindi equivale a k.
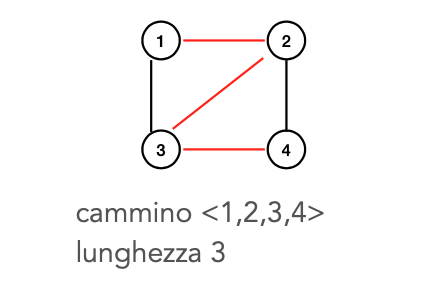
Il cammino di divide in due versioni:
- cammino semplice che non contiene nodi ripetuti
- cammino non semplice che contiene nodi ripetuti
Il ciclo è un cammino dove . Anche il ciclo si divide in semplice e non. Vedi grafo diretto aciclico.
Proprietà di connessione Si dice grafo connesso un grafo se esiste un cammino che connette ogni coppia di nodi del grafo.
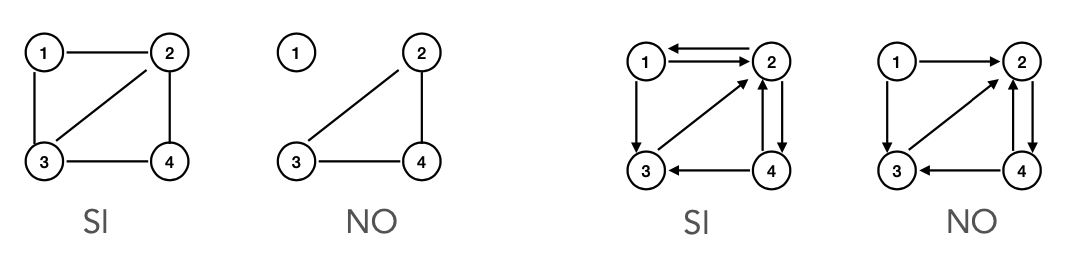
Si dice grafo fortemente connesso se esiste un cammino diretto che connette ogni coppia di nodi del grafo.
Sottografo
title: Sottografo
$G'=(V', E')$ è un sottografo di $G=(V, E)$ se $V' \subseteq V \mbox{ e }E'\subseteq E$.I sottografi possono a loro volta essere connessi o fortemente connessi, anche se il grafo di partenza non lo è. Questi sottografi connessi si dicono componente connessa o componente fortemente connessa.
Componente connessa è un sottografo connesso ed è massimale, ovvero non esiste un sottografo connesso di di che includa tale che
Componente fortemente connessa è un sottografo fortemente connesso ed è massimale, ovvero non esiste un sottografo connesso di di che includa tale che
Le dimensoini del grafo sono:
- numero di nodi
- numero di archi
title: Attenzione
Il costo computazionale solutamente è espresso in termini di $O(n+m)$.Un grafo si dice completo se esiste un arco per ogni coppia di nodi. In generale, per un grafo completo non orientato, si ha che il numero di archi è . Invece, per un grafo completo orientato il numero di archi è . Entrambi sono dell’ordine di grandezza di .
Si dice che un grafo è sparso se ha pochi archi, . In questo caso conviene utilizzare liste di adiacenza.
Si dice che un grafo è denso se ha molti archi, . In questo caso conviene utilizzare matrici di adiacenza.
Un albero libero è un grafo aciclico connesso, tale che .
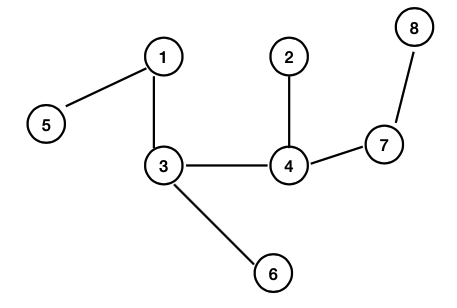
In un albero libero si può designare una radice, e considerare gli archi orientati dai padri ai figli, facendolo diventare così un albero radicato.
Più alberi liberi formano una foresta, tale che .
Rappresentazione
Matrice di adiacenza
Matrice G
dove è l’indice della riga e quello della colonna.
Se il grafo è non orientato, la matrice è simmetrica.
Il costo del controllo della presenza dell’arco è di , mentre il quello per l’elenco dei vicini di un nodo è .
Liste di adiacenza
La lista di adiacenza è un array G di liste.
G[v] è un puntatore alla lista che contiene tutti i vicini di v.
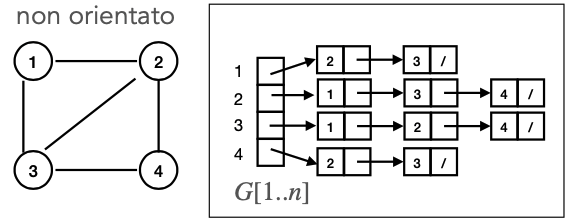
Lo spazio richiesto per questa struttura è .
Costo controllo presenza arco: Costo elenco vicini nodo:
Per iterare su tutti i nodi del grafo si può semplicemente utilizzare
for all v ∈ V do
nodo v
Per iterare sugli archi si può usare
for all (u, v) ∈ E do
arco (u, v)
Per iterare sui nodi e accedere agli archi incidenti:
for all v ∈ V do
for all (v, u) ∈ E do
arco (v, u)
Per la visita di un grafo esistono due algoritmi: