Two party key exchange

Protocollo di scambio di chiavi basato sulla crittografia asimmetrica.

L’obiettivo è quello di scambiare chiavi su un canale non sicuro.

Questo protocollo nasce nel 1974 con Ralph Merkle. È basato sulla crittografia simmetrica.

Merkle Puzzle

Si hanno due schemi:

• Uno schema simmetrico sicuro E
• Uno schema simmetrico non sicuro W, che può essere rotto in un tempo N

Si compone di 7 passi:

1. A genera N chiavi per lo schema sicuro E, associando ad ognuno un id $(1,K_1),(2,K_2),(3,K_3),...$
2. A cifra tutti gli N messaggi con lo schema debole W
3. Mescola tutti gli N messaggi cifrati e li invia a B. Eve vede passare N messaggi cifrati
4. B sceglie un messaggio random tra gli N che ha ricevuto
5. B spende un tempo N per rompere W, ottenendo l’id e la chiave scelta casulamente il passo prima. $(X,K_X)$
6. B invia ad A l’id della chiave scelta
7. A recupera la chiave tra quelle che ha generato in precedenza, e quindi entrambi hanno la chiave di crittografia simmetrica

Che garanzie di sicurezza ci da?

Eve, per avere la chiave, spende N per rompere la cifratura debole, per una media di N/2 messaggi, per trovare X. In totale quindi Eve deve spendere $\frac{N^2}{2}$ di tempo per trovare la chiave scelta da B. Il costo non è esponenziale, ma quadratico.

Questo tipo di approccio però non è utilizzabile al giorno d’oggi perché non è esponenziale, quindi troppo poco sicuro.

Logaritmo discreto

Anzichè utilizzare un algoritmo di cifratura simmetrica, si è pensato di utilizzare il logaritmo discreto su campi finiti con cardinalità un numero primo di grandi dimensioni.

$Z_{11} \to \{0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10\}$
$3^7 \mod 11 = 9$
Data la base 3 (*generatore* pubblico, come il modulo 11) e il risultato 9 (inviato), è difficile calcolare l'esponente 7.
Gli algoritmi che esistono per calcolare l'esponente, sono tutti di costo esponenziale.
 
Questo algoritmo può essere costruito con numeri interi, o con altri gruppi matematici, come ad esempio le **elliptic curves** (curve discrete). Con queste curve si possono definire gruppi ciclici per scopi crittografici.

Solitamente, negli standard, si astraggono le descrizioni dei protocolli, e si utilizzano i simboli $g$, che rappresenta il generatore (nell’esempio di prima il 3), e $p$ rappresenta il grippo ciclico di ordine primo ($Z_{11}$).

• Problema del logaritmo discreto: “if you want to use $g^a$”, it is hard to compute $a$.

Diffie-Hellman Key Exchange

Protocollo di scambio di chiavi Diffie-Hellman. I protocolli che iniziano con DH sono tutti protocolli Diffie-Hellman. Se inizia con ECDH, è un protocollo Diffie-Hellman basato su Elliptic Curves.

Computational Diffie-Hellman

Dati $g^a$ e $g^b$ è difficile calcolare $g^{ab}$.

Decisional Diffie-Hellman

Dati $g^a$ e $g^b$ è difficile riuscire a distinguiere $g^{ab}$ da $g^r$, dove $r$ è random. $a\text{mbox}eb$ possono essere numeri qualsiasi, e solitamente si utilizzano numeri molto grandi (hanno i bit significativi settati a 1). Solo i numeri in $p$ devono essere numeri primi. $g$ e $p$ sono pubblici.

1. A genera $g^a$
2. B genera $g^b$
3. A e B si scambiano $g^a$ e $g^b$
4. A si calcola $(g^b{)}^a$ e B si calcola $(g^a{)}^b$

Come detto sopra, anche se Eve riesce a vedere $g^a$ e $g^b$, non riuscirà mai a calcolare $g^{ab}$ e non riuscirà nemmeno a distinguerlo da random.

Quindi $g^{ab}$ si può utilizzare come chiave. Dal momento che non si è riuscito a trovare un algoritmo che calcoli questo numero in modo efficiente, il protocollo è da considerarsi sicuro.

$g^{ab}$ sarà utilizzata come chiave simmetrica.

Curve ellittiche

Al giorno d'oggi si utilizzano soltanto le curve ellittiche. Gli altri metodi basati sui numeri interi sono tutti deprecati, perché sono vulnerabili a certi tipi di attacchi e bisognerebbe prendere dei numeri molto più grandi per ottenere lo stesso livello di sicurezza.
 
$\Rightarrow$ le curve ellittiche sono molto più veloci dei numeri interi a parità di sicurezza

L’aritmetica modulare può implementare gruppi sicuri, usando $(a\ast b)\mathrm{mod}p$, dove p ha alcune caratteristiche, come ad esempio essere primo.

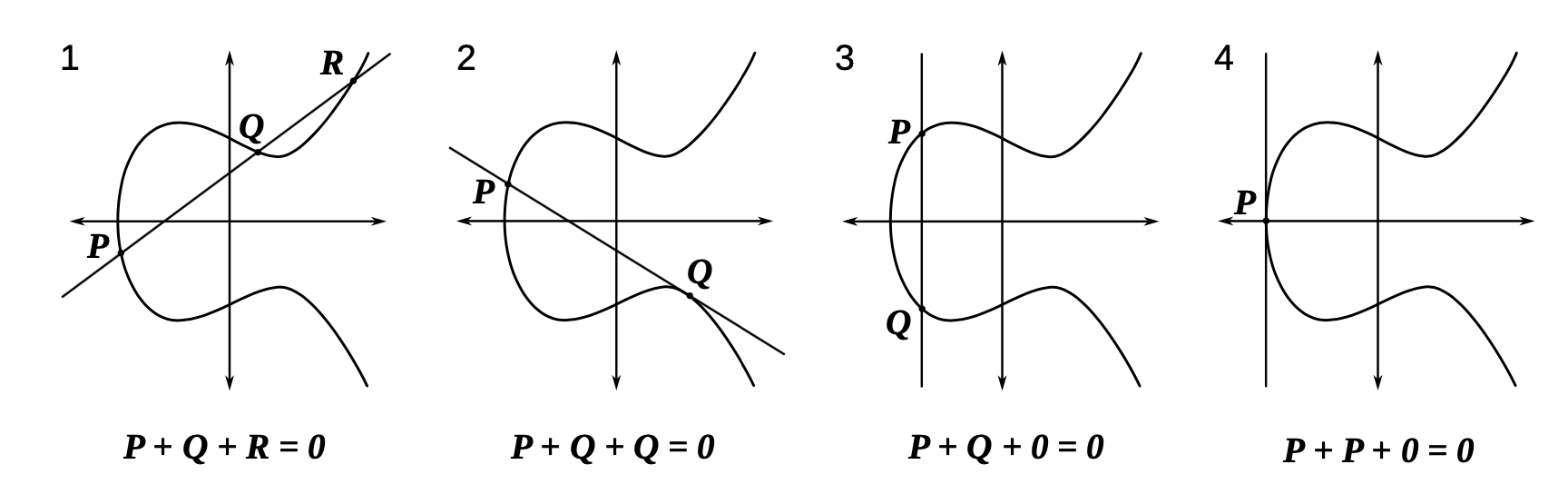
Astraendo la matematica, i protocolli creati su alcune congetture di difficoltà possono essere implementati usando sia la matematica modulare che le curve ellittiche. $g^a$, dove g è un intero, e l’operazione è un’esponenziale modulo p

Con le elliptic curves, si ha $a\ast g$, dove g è un punto sulla curva ellittica, e l’operazione è una moltiplicazione di un punto sulla curva.

Le curve standardizzate dal NIST sono:

• P224, con una sicurezza di 112 bit
• P256, con sicurezza di 128 bit
• P521, con sicurezza poco più di 256 bit

Esistono anche degli standard IETF con:

• Curva 25519 e Curva 448, dove il protocollo Diffie-Hellman prende il nome di X25519 e X448.

csec_0205