Disjoint set

Il disjoint set memorizza una collezione di sottoinsiemi disgiunti di un insieme generativo. Ammette operazioni di ricerca e unione, ma non inserzione e cancellazione.

Un insieme generativo è un insieme del tipo $X=\{1,2,...\}$. I sottoinsiemi disgiunti sono sottoinsiemi di un insieme generativo, del tipo $S=\{S_1,...,S_k\}$ tale che

• $S_i\subseteq X\forall i=1,...,k$
• $S_i\cap S_j=\varnothing \forall i\ne j,\text{mbox}i,j=1,...,k$
• ${\cup }_{i=1}^k{S}_i=X$

Primitive

• make-set(X): restituisce un disjoint set in cui $S_i=\{i\},\forall i=1,...,|X|$ - $O(n)$
• find-set(DS, x): restituisce un rappresentante dell’insieme a cui appartieen x - $O(n)$
• union(DS, x, y): unisce gli insiemi a cui appartengono x, y - $O(n)$

Ogni insieme è rappresentato da un albero, e quindi per ogni insieme esiste un rappresentante che fa da radice dell’albero.

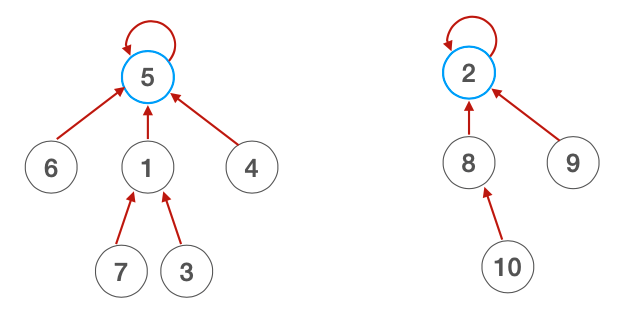
make-set(X):
	DS := new_array[1..n]
	for i=1 to n do
		DS[i] := 1
	return DS

Costo computazionale $O(n)$

find-set(DS, x):
	if DS[x] = x then
		return x
	else
		return find-set(DS, DS[x])

Costo computazionale lineare all’altezza dell’albero. $O(n)$

union(DS, x, y):
	xr := find-set(DS, x)
	yr := find-set(DS, y)
	if xr != yr then
		DS[xr] := yr

Anche in questo caso il costo computazionale è lineare all’altezza dei due alberi, quindi il costo è di $O(n)$

Rango

Ogni albero ha un rango, che rappresenta la sua altezza. Il Disjoint set, quindi, mantiene un array di rank, e un array di padri.

make-set(X):
	DS.p := new_array[1..n]
	DS.rank := new_array[1..n]
	for i=1 to n do
		DS.p[i] := 1
		DS.rank := 0
	return DS

find-set(DS, x):
	if DS.p[x] = x then
		return x
	else
		return find-set(DS, DS[x])

union(DS, x, y):
	xr := find-set(DS, x)
	yr := find-set(DS, y)
	if xr != yr then
		if DS.rank[xr] > DS.rank[yr] then
			DS.p[yr] := xr
		else
			DS.p[xr] := yr
			if DS.rank[xr] = DS.rank[yr] then
				DS.rank[yr] := DS.rank[yr] + 1

Utilizzando l’euristica del rango, un albero della foresta con radice r ha almeno $2^{rank[r]}$ nodi, quindi un albero di radice r con k nodi ha $k\ge 2^{rank[r]}$ $\log k\ge rank[r]$

Il costo computazionale di find e union, usando il rango, è di $O(\log n)$.

Perchè? Caso base: subito dopo make-set, prima della union si ha

• ogni albero ha esattamente un nodo $\Rightarrow 1\Rightarrow 2^0$
• per ogni nodo r si ha rank[r] = 0 $2^{rank[r]}\le 1$

Ipotesi induttiva: dopo $t\ge 0$ operazioni union, per un albero di $k\le n$ nodi con rappresentante r vale che $2^{rank[r]}\le k$. Per xr = yr è vero. Se invece xr != yr, allora

• rank[xr] > rank[yr]: xr diventa il rappresentante di yr, ma il rango no cambia
• rank[xr] < rank[yr]: yr diventa il rappresentante di xr, ma il rango no cambia
• rank[xr] = rank[yr]: $|S_x\cup S_y|=|S_x|+|S_y|\ge 2^{rank[xr]}+2^{rank[yr]}=2^{rank[yr]+1}$ make-set costa sempre $O(n)$, mentre union e find-set costano $O(\log n)$

asd_35