Problema dello zaino

Input: zaino di capacità $W\ge 0$, $n$ oggetti $1,2,3,...,n$, pesi $w_1,w_2,...,w_n\in N$, valore $v_1,v_2,...,v_n\in N$ Output: selezionare degli oggetti con somma dei pesi totale minore o uguale a $W$ e che massimizzi il valore totale degli oggetti selezionati.

La soluzione ammissibile è: selezione degli oggetti $i_1,i_2,...,i_k$ tale che ogni $i_t\in [\mathrm{1...}n]$ e ${\sum }_{t=1}^k{w}_t\le W$.

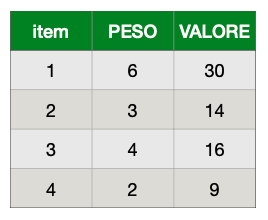
Esistono due varianti di questo problema:

• con ripetizione: lo stesso oggetto può essere selezionato più volte
• senza ripetizione: lo stesso oggetto può essere selezionato una sola volta

Il problema ha una sottostruttura ottima, e per questo si potrebbe utilizzare un algoritmo greedy.

Versione greedy

Ci possono essere vari modi per ordinare gli oggetti, per poi sceglierli iterativamente per inserirli nello zaino, ma non esiste un algoritmo greedy abbastanza buono da poter essere utilizzato, perché in qualche modo sbaglia sempre (vedere le slide per esempi concreti).

Versione programmazione dinamica

Come sottoproblema si può vedere: Per ogni $w\in N$ tale che $w\le W$, definiamo $K(w)=$ massimo valore ottenibile con zaino di capacità $w\le W$.

$K(w)={\max }_{i:w_i\le w}\{v_i+K(w-w_i)\}$

Versione con ripetizione.

Il caso base è composto da $w=0\to K(0)=0=$ massimo valore ottenibile con uno zaino di capacità 0. Soluzione al problema originale: $w=W\to K(W)=$ massimo valore ottenibile con uno zaino di capacità W.

Per calcolare il valore della soluzione ottima si ha:

K[0] := 0
for w = 1 to W do
	K[w] = max(i:wi <= w) {v1 + K(w-wi)}

Peso $O(Wn)$ pseudo-polinomiale

Versione senza ripetizione

Il sottoproblema ha quindi una ridotta capacità dello zaino, e una ridotta scelta di items.

Per ogni $w\in N$ tale che $w\le W$ e per ogni $j=1,2,...,n$ definiamo $K(w,j)=$ massimo valore ottenibile con zaino di capacità $w\le W$ potendo scegliere solo tra gli oggetti $1,2,...,j$.

Se $j$ non sta nella soluzione ottima, allora si ha $K(w,j)=K(w,j-1)$. Se invece $j$ sta nella soluzione ottima, allora si ha $K(w,j)=v_j+K(w-w_j,j-1)$.

Se non sappiamo se $j$ è presente o meno nella soluzione, si ha

$$K(w,j)=\max \begin{array}{c}\{\begin{array}{ll}K(w,j-1)& \\ v_j+K(w-w_j,j-1)& \text{mbox}se{w}_j\le w\end{array}\end{array}$$

max_val_zaino(n, pesi, valori):
	for j = 0 to n do
		K[0, j] := 0
	for w = 0 to W do
		K[w, 0] := 0
	for j = 1 to n do
		for w = 1 to W do
			if pesi[j] > w then
				K[w, j] := K[w, j-1]
			else
				K[w, j] := max{K[w, j-1], valori[j] + K[w-pesi[j], j-1]}
	return K[W, n]

Il costo computazionale è di $O(W\cdot n)$

asd_39asd_40