Strategie di pivoting

• Teorema di fattorizzazione di Gauss con scambio di righe
  • Applicazione
    • Passo 1
    • Passo 2
  • Soluzione
  • Non unicità della fattorizzazione
• Strategia di pivoting parziale
  • Costo computazionale
• Pivoting totale
  • Costo computazionale

Teorema di fattorizzazione di Gauss con scambio di righe

Teorema

Se $A$ è non singolare, allora esistono una matrice di permutazione P, una matrice triangolare superiore U e una matrice triangolare inferiore L con diagonale unitaria tali che $PA=LU$

L’idea alla base è invertire righe della matrice durante il procedimento di fattorizzazione nel Metodo di Gauss. Se gli stessi scambi vengono applicati anche al termine noto, equivale a scambiare due equazioni nel sistema $Ax=b$.

Al passo k si invertono le righe k e r della matrice $A_k$, con $r\ge k$, per non rovinare la struttura triangolare che si sta costruendo.

Attenzione

Dal punto di vista tecnico basta che il pivot sia diverso da zero. Dal punto di vista numerico, si possono fare delle scelte più vantaggiose di altre, dal momento che la scelta grava sulla matrice $L$, che diventa instabile quando gli elementi del triangolo sono molto grandi rispetto alla diagonale.

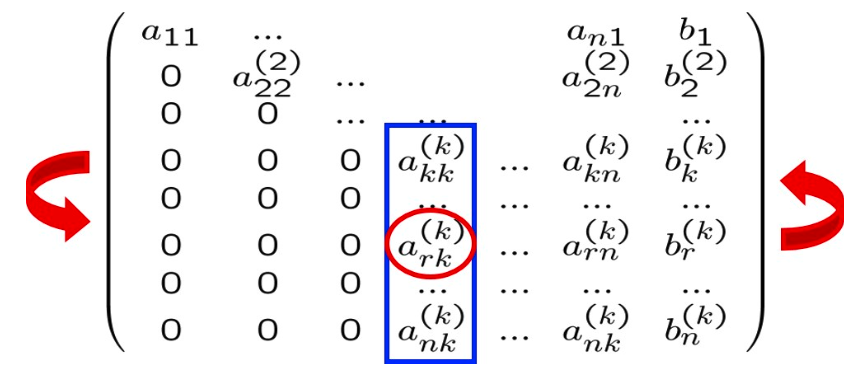
Successivamente allo scambio, si procede con la fattorizzazione di Gauss.

Lo scambio delle righe è realizzato utilizzando le Matrici di permutazione.

Applicazione

Passo 1

$$A=\left(\begin{array}{cccc}{a}_{11}& a_{12}& ...& a_{1n}\\ a_{21}& a_{22}& ...& a_{2n}\\ ...& & & \\ a_{n1}& a_{n2}& ...& a_{nn}\end{array}\right)$$

Dall’ipotesi di non singolarità del Metodo di Gauss, si ha che esiste almeno un elemento diverso da zero nella prima colonna di A.

1. Si definisce la matrice di permutazione elementare $P_1$ che scambia la riga 1 con qualsiasi riga r tale che $a_{r1}\ne 0$.
2. Si calcolano i moltiplicatori per la prima colonna della matrice $P_{1}A$ e si definisce $L_1$
3. Si aggiornano gli elementi della matrice $A_2=L_1{P}_{1}A$

Passo 2

Si va a lavorare la matrice ${\tilde{A}}_2$, sottomatrice di $A_2$, formata dalle sue ultime $n-1$ righe e colonne. Si osservi che:

• $A_2$ è non singolare, perchè prodotto di matrici non singolari
• Per il Teorema di Laplace, si ha che il $det(A_2)=a_{11}^{2}det({\tilde{A}}_2)$
• $det(A_2)\ne 0$ e $a_{11}^{(2)}\ne 0$, implica che anche $det({\tilde{A}}_2)\ne 0$, quindi ${\tilde{A}}_2$ non singolare Segue che $a_{i2}^{(2)}\ne 0$ per almeno un indice $i$.

Soluzione

$$\begin{array}{r}Ax=b\\ PAx=Pb\\ LUx=Pb\\ \{\begin{array}{l}Ly=Pb\\ Ux=y\end{array}\end{array}$$

Non unicità della fattorizzazione

Osservazioni

La fattorizzazione $PA=LU$ non è unica. Ad ogni passo si può scegliere una permutazione differente, che può cambiare la fattorizzazione finale.

Strategia di pivoting parziale

Usato nella pratica perché ha un buon rapporto costi-benefici.

Osservazione

La strategia di pivoting parziale rende l’algoritmo di soluzione del metodo di Gauss più stabile.

Al passo k si sceglie l’elemento in valore assoluto più grande della prima colonna della matrice ${\tilde{A}}_k$.

Questo porta ad avere:

$$|m_{ik}|\le 1,\forall k=1,...,n-1,\forall i=k+1,...,n$$

Costo computazionale

Al pasos k si devono effettuare $n-k+1$ confronti, che hanno un un costo di $O(\frac{n^2}{2})$.

Pivoting totale

Al passo $k$ si sceglie l’elemento in valore assoluto più grande della sottomatrice ${\tilde{A}}_k$.

Porta quindi ad avere una composizione del tipo $PAQ=LU$, con $Q$ la matrice di permutazione per scambiare le colonne.

Costo computazionale

Il costo computazionale è comparabile a quello della fattorizzazione.

Osservazione

Se $A$ è strettamente diagonale dominante per righe o colonne, allora la condizione del pivoting partiale è soddisfatta.