Algoritmo di Dijkstra
Un algoritmo per calcolare l’albero dei cammini minimi di un grafo è l’algoritmo di Dijkstra, dal momento che la semplice BFS non basta.
title: Osservazione
Un cammino con più archi più essere più corto in termini di peso di uno con meno archi.flowchart LR
0((1)):::someclass -.4.-> 1((2)):::someclass -.2.-> 2((4)):::someclass
3((1)):::someclass -.2.-> 4((3)):::someclass -.1.-> 5((2)):::someclass -.2.-> 6((4)):::someclass
classDef someclass fill:#f96, color:#fff
Durante la BFS il nodo 3 riporta al nodo 2 con un cammino più corto.
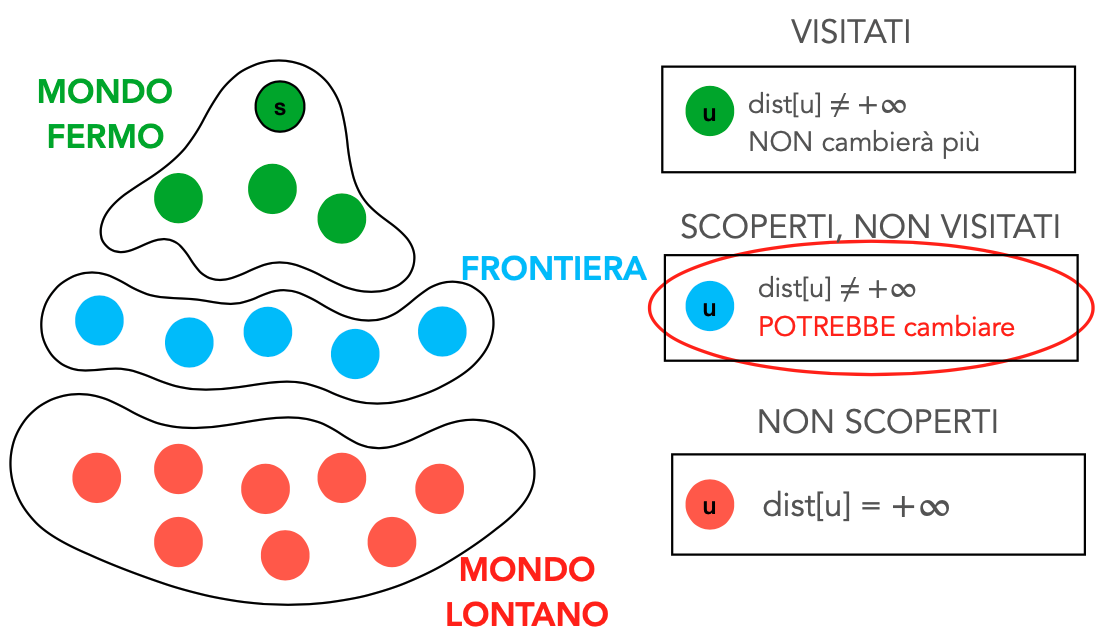 Dalla frontiera (coda con priorità) si prende il nodo che costa di meno in termini di cammino (
Dalla frontiera (coda con priorità) si prende il nodo che costa di meno in termini di cammino (dist[v]). Una volta che un nodo dalla frontiera viene spostato nel mondo fermo, non si può tornare indietro.
Un nodo è visitato quando si sono esplorati tutti i vicini.
Il nodo da esplorare successivamente è scelto dalla lista dei nodi scoperti ma non ancora esplirati con dist[] minima.
Dijkstra(G, c, s):
for all u ∈ V do
dist[u] := +∞
prev[u] := 0
dist[s] := 0
q := new_priority_queue({(v, dist[v])|v=1, ..., n})
while not is_empty_queue(q) do
u := dequeue(q)
for all (u, v) ∈ E do
if dist[v] > dist[u] + c(u, v) then
dist[v] := dist[u] + c(u, v)
prev[v] := u
decrease_priority(q, v, dist[v])
return prev[]
calcola il costo tra due nodi.
Il costo di Dijkstra è di . Se la coda si implementa con un heap binario, il costo si alza a
L’alternativa a questo algoritmo per pesi negativi, è l’algoritmo di Bellman Ford.